[置顶]李瑞远-浮点时序数据压缩(全文演讲词+PPT)
(本文根据2025年7月5日时序数据库技术创新大会上的演讲整理)
大家好!我是重庆大学李瑞远,我的演讲题目是《浮点时序数据压缩》。刚刚几位老师课题非常大(注:前面的演讲者北邮计算机学院院长王尚广教授讲的是“卫星计算”),然后我就从另一个角度,我从小的角度来讲,我是越小越好。压缩我们就希望它压缩后的空间越小越好。
最开始我提交这个报告的时候,会议的组织方秦老师就跟我说,这个题目太学术了,能不能改一下。我后面想了想,还是别改了,为什么呢?首先我们这个场是一个学术报告场。第二,我们学校大一的本科生要进我的实验室,我就让他们看我这几篇文章,他们基本上都能看懂,所以我相信你们都能听懂,如果听不懂是我的问题,我没讲好来。

大家应该都是搞时序数据的,对时序数据都非常了解,所以时序数据的很多例子我就不说了。我其实是做时空数据研究的,我为什么突然之间做时序数据研究了呢?其实我最开始的时候想要做的是轨迹数据压缩,轨迹数据里面有经度、有纬度,它们也可以看作是浮点类型的时序数据。在做的时候,我发现我的方法在普通的、通用的时序数据上也能够适用,所以我一下子就进入这个领域。

海量的浮点时序数据以流式的方式源源不断地产生。高效的、紧凑的,无损或是Error-Bounded的浮点时序数据的压缩非常有用,为什么呢?因为它能够减少传输带宽,减少存储空间。如果在压缩时能够保证没有信息损失,在很多场景里面非常有用,比如说我们IoTDB数据管理的领域里面,用户用咱们的IoTDB,你作为数据库的开发人员,你不能改变用户的任何数据。你如果擅自修改用户的数据,他可能会跟你急,是吧?当然在有些场景里面,Error-Bound压缩,也就是误差有界压缩,也是有用的,后面我们也会说。

我们先看看浮点数据的底层存储结构。时序数据大部分都是浮点类型的。整数的存储格式大家都非常清楚,而浮点数的存储格式比较复杂。这是一个double类型的存储格式,64位的。它有一位符号位(0表示正数,1表示负数),以及11位的指数位和52位的尾数位。在底层它还分成了很多种不同的类型,我们通常看到的大多数都是正常数。给定一个底层的二进制存储,它到底代表我们生活中看到的多大的数据呢?就是按这个公式计算的,这个公式很复杂,我们也不展开了。当然我们还有其他的一些数据类型,比如说零、无穷大、无穷小、Not a Number (即Java里面的NaN)、以及次正规数。次正规数也有类似的一个计算方式。这里我们主要是聚焦在正规数和零这两类数据上,但是我们后面讲的方法,其实都能很容易地扩展到其它类型的数据上。

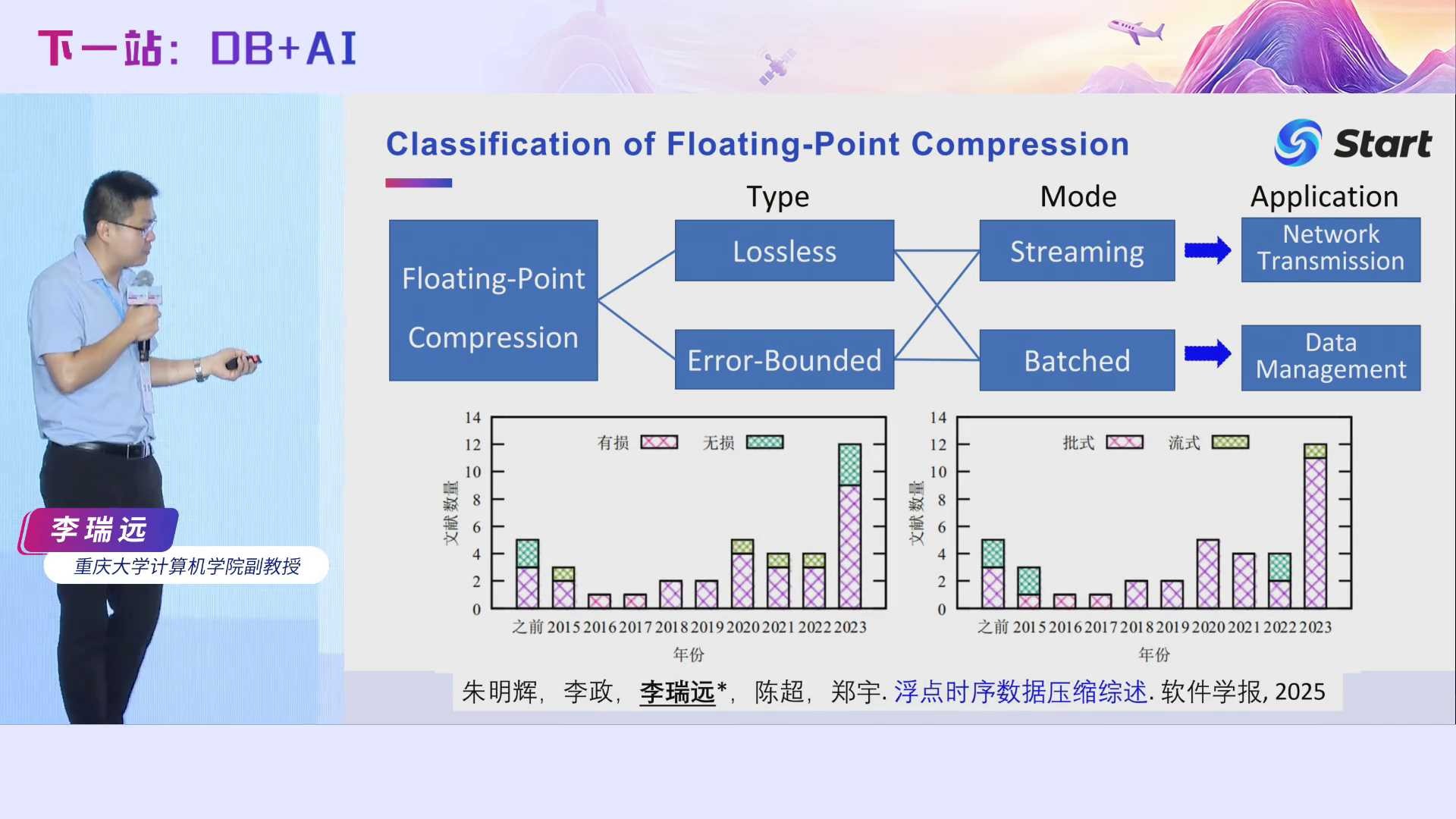
整个浮点数据的压缩可以分成以下几种类型。首先根据是否有信息损失,我们可以分成lossless和Error-Bounded。然后根据它的压缩模式,可以进一步分为流式和批式。一个典型的流式压缩应用场景是网络传输,为什么呢?因为我们的IoT设备源源不断地产生浮点类型的时序数据。一般情况在传输之前,我们希望对它进行压缩,从而减少传输带宽占用,但是数据源源不断地产生的,你不可能把所有的数据都接下来,你再统一压缩,然后再传出去。这会带来较大的网络延时,也对内存有较高要求。批式压缩的应用场景更多,比如IoTDB中的数据管理,它可以对数据缓存起来,然后再压缩。当然,在数据传输时,也可以用Mini-batch压缩。我这边说的流式是指严格的流式,即数据一来立刻压缩,然后立即传出去,这能够减少后面操作的延迟。我们最近发了一篇论文,对现有时序压缩算法做了一个综述,发表在了今年的软件学报上,大家感兴趣的话可以去看看。
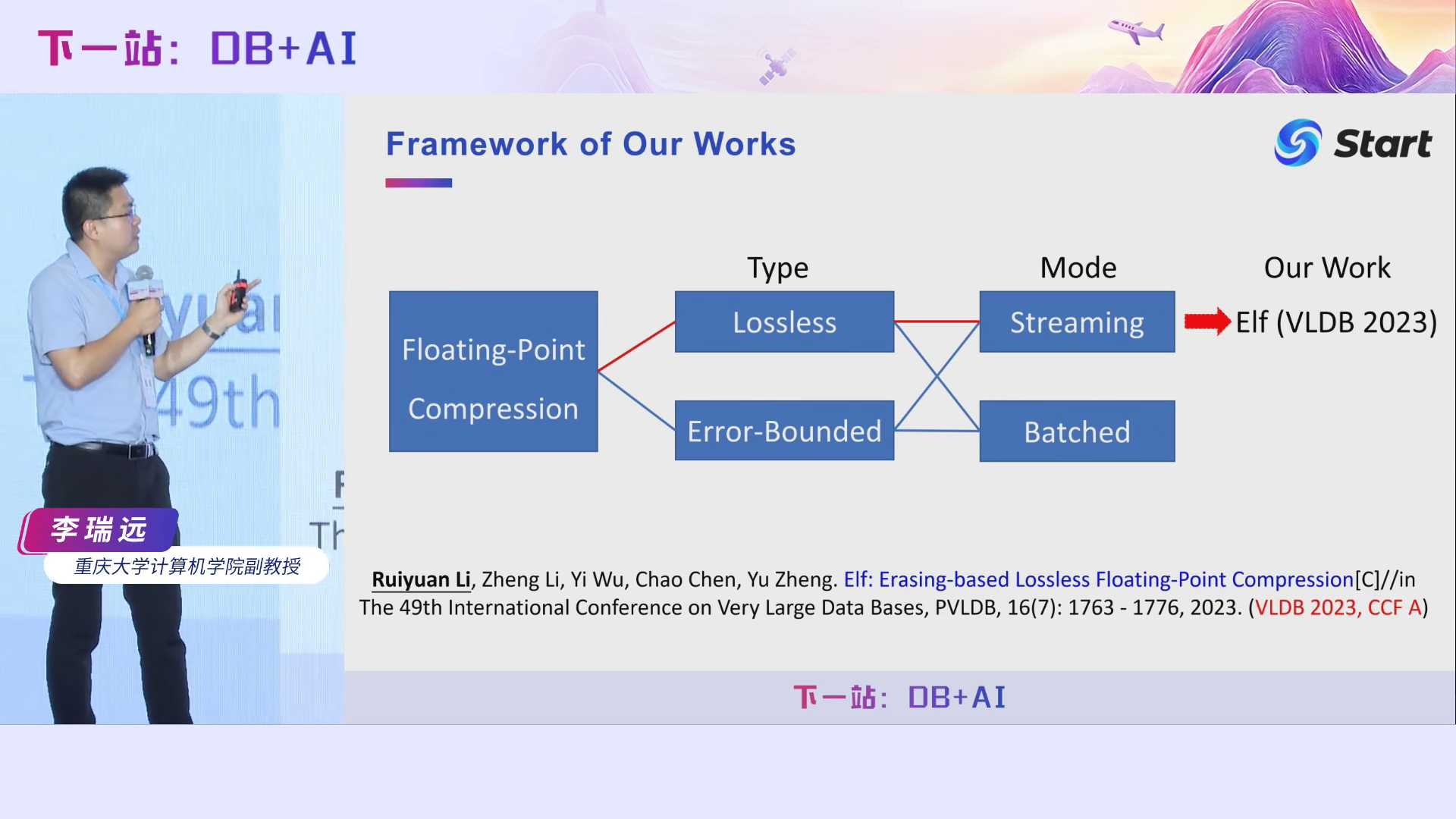
我们首先来讲一个流式无损压缩算法,发表在了2023年的VLDB会议上。
在当时,也就是2023年之前,浮点时序压缩算法大体可以分成三类。首先是通用的压缩算法。通用压缩算法,比如GZip、Zstd等,也可以压缩时序数据,但是它们通常是批式的,当时序数据源源不断地到来时,它们首先需要将数据缓存下来,然后再压缩,在mini-batch的情况下,压缩率不好。此外,这些方法没有充分挖掘浮点数底层的特征,压缩效率也不佳。第二类是有损浮点压缩算法,例如ZFP和MDZ,但是在一些场景里面信息损失是不可忍受的。第三类是无损浮点压缩算法,当时比较著名的是Gorilla和Chimp,但是这些这算法压缩效果不是很好。我们来分析一下它们为什么不好。
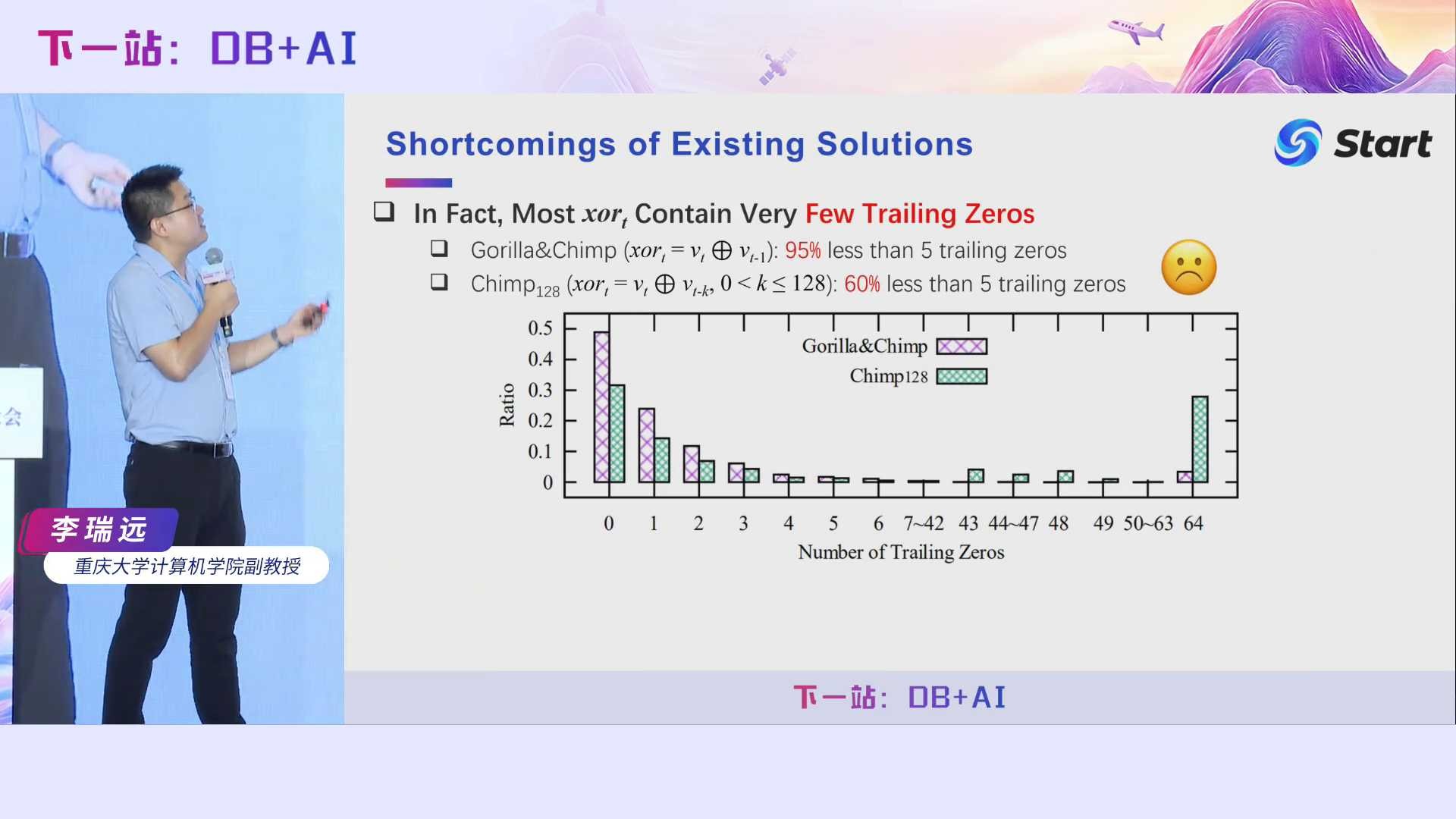
Gorilla和Chimp主要基于异或操作。异或操作大家肯定都非常清楚,大一的时候我们就学了相同为零、相异为一是吧?根据我们前面浮点数底层存储结构的介绍,3.17和3.25它们在底层的存储格式长这样。我们对它们进行异或操作后,得到一个异或值长这样。异或值前面这些零就叫前导零,后面这些零就是尾随零。我们在压缩的时候,只要记录前导零的个数以及尾随零的个数,再原封不动地记录中间位。前导零的个数为14,只需要4个比特存储;尾随零的个数为2,只需要1个比特存储;加上中心位的比特数,总共加起来通常要少于64位,这就达到了一个压缩效果。这里我们也可以看到,前导零和尾随零越多,中心位就越少,压缩效果就越好。在解压的时候,我们只要拼一些前导零,拼一些尾随零,然后原封不动地恢复中心位,就达到了无损解压的目的。

Gorilla假设异或值的前导零和尾随零都非常多。在大多数情况下,前导零的确会非常多,因为在时序数据里面,相邻的两个数之间相差不会太大。比如说气温,上一时刻和下一时刻气温相差不会太大,它们异或之后前导零会非常多。但是尾随零真的会很多吗?我们做了一些实验发现,两个相邻的时序数据进行了异或之后,95%以上的情况下尾随零个数都是小于5的,也就是说压缩效果并不好。即使是Chimp128,它不再直接跟前面那个数进行异或,而是跟前面128个数分别进行异或,然后选择一个产生尾随零最多的数。即使这样,仍然有60%的情况都少于5个尾随零的,这同样导致它的压缩率是非常低的。因此提高尾随零的个数,对提升压缩效果是非常有用的。
我们的基本思想非常简单,如果能够擦除每个浮点数后面的一些比特位,即将他们置为零,那么两个拥有很多尾随零的浮点数进行异或操作后,异或值的尾随零也非常多。比如,对于3.17,我们擦除它后面44个比特位,得到一个数字3.1640625,再跟本来有很多尾随零的3.5进行异或操作,得到的异或值同样有很多尾随零。在解压的时候,因为我们前面说了,我们需要无损压缩,既然你擦除了一些比特位,你就会丢失一些信息,我们要怎么恢复它们呢?我们有幸发现了一个规律。首先,我们可以通过拼接得到异或值Δ’,然后Δ’与3.25执行异或操作后,得到3.1640625。关键点在于,我们如何通过3.1640625得到3.17。假设我们知道原来的那个数小数点后面有两个数字,也就是说它的精度是2(即10-2=0.01),而且我知道擦除后的值肯定比原来那个值要小,并且擦除前后两个数之差小于10-2,那么我们就可以把3.1640625的40625直接擦掉,然后给它加上0.01,就能够得到3.17。它本质上是一个保留精度的向上取整操作。通过这个公式,我们就可以实现无损解压了。
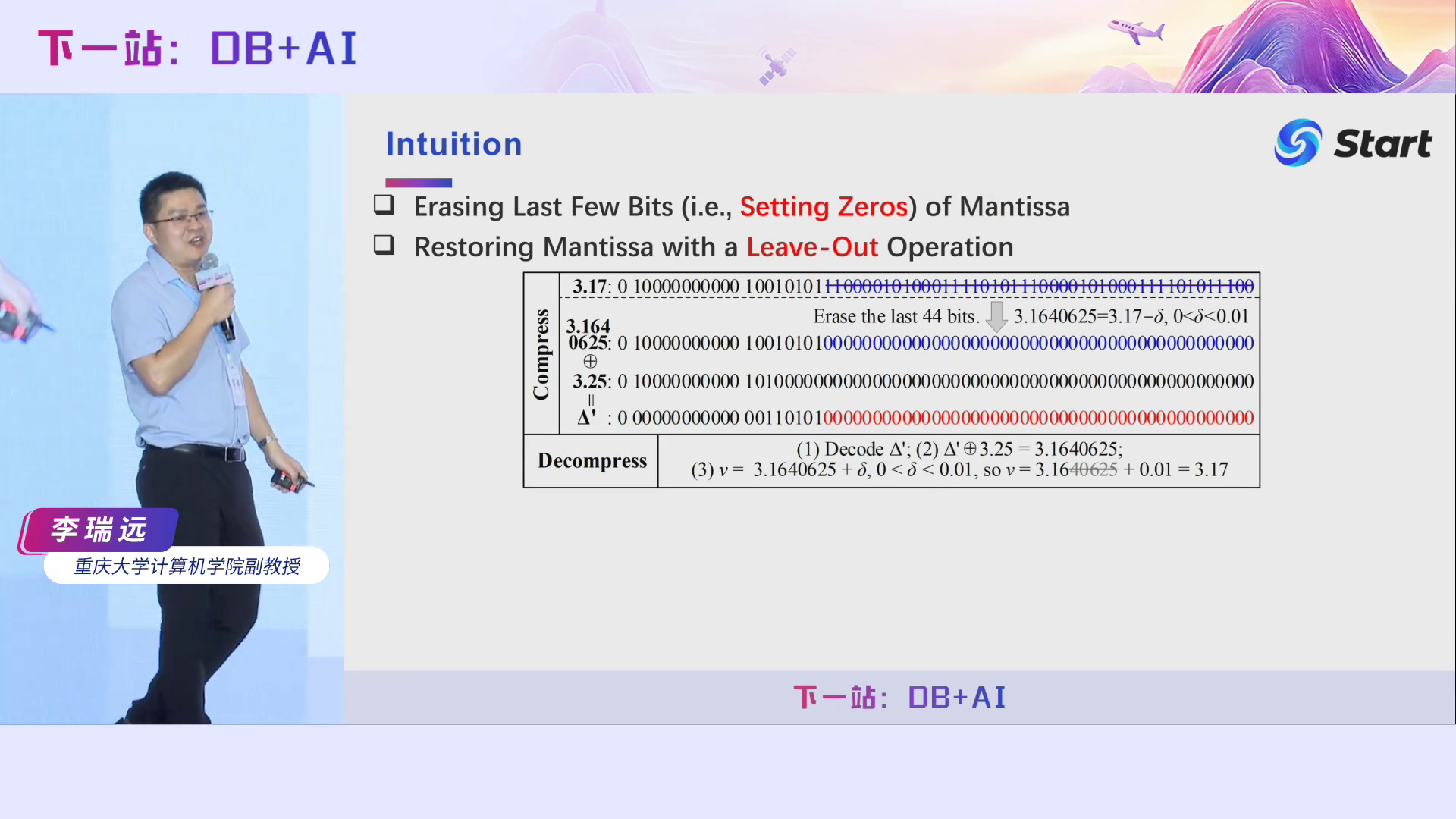
这就是我们方法Elf的大体思想。我们为什么叫Elf呢?它有两层含义,一个是方法英文首字母缩写,即Erasing-based Lossless Floating-point compression;另一层即它的英文含义是小仙女、小精灵。我们提出的方法非常轻便,只需最简单的位操作和基本的算数操作。此外,它还像小仙女一样有魔法,能够让异或值的尾随零个数从2增加到44,还有破镜重圆的魔力,能够让丢失的信息给变回来。因此,这个名字是一语双关的。我们的Elf算法还能够以流式的方式执行,因为我们只需要看前一个数就行了。当一个数来了之后,我们先对它进行擦除操作,然后与前一个擦除后的数进行异或操作,再对异或后的值进行编码压缩即可。在解压的时候,同样可以以流式的方式进行。

算法思想非常简单,但是这里面的水很深,怎么个深法呢?首先我们如何能够保证效率问题,如何能够快速地决定擦除哪些比特位?第二个是如何编码异或值?也就是怎么压得更狠。第三就是如何快速恢复原来的数?大体思想我前面都说了,但是里面还有很多小细节,需要我们进一步理清。

首先是效率问题。在介绍方法之前,我先说几个我们在初中就知道的一些知识。比如说给你一个小数,它的精度就是小数点后面精确到几位,我们记为α。比如,3.17的精度是2,-0.0317的精度是4。此外,我提出了一个新的概念,就是尾随前缀数,这个概念也比较简单,比如说原始的数据是3.17,我逐个擦除它后面的比特位,每擦一个,它就变成了另外一个数,这个数称为3.17的尾随前缀数。你看3.17,它有好多尾随前缀数,对吧?

我们不断地尝试擦除新的比特,直到我们找到一个符合我们条件且效果最好的尾随前缀数。需要满足哪些条件呢?即擦除后得到的数与原来的数的差值小于10的α次方,α就是前面说的精度,并且擦除的位数越多越好。最简单一个方式就是,我不断地往下擦,然后再验证得到的数是否满足差值条件,如果满足,我们继续往下擦,直到不满足差值条件为止。最后一个满足差值条件的数就是所求。但这样效率会非常低,即O(52),也就是说,我们可能会尝试52次擦除,因为我们共有52个尾随前缀数。为此,我们给出了一个公式,可以直接计算出我应该从哪里擦除得到的尾随零是最多的,与此同时满足我们前面所说的差值条件。这里给出了一个例子,对于3.17,它的α是2,代入这个公式,可以得到g(α)为8,也就是说,我们需要擦除52-8=44位的比特位。

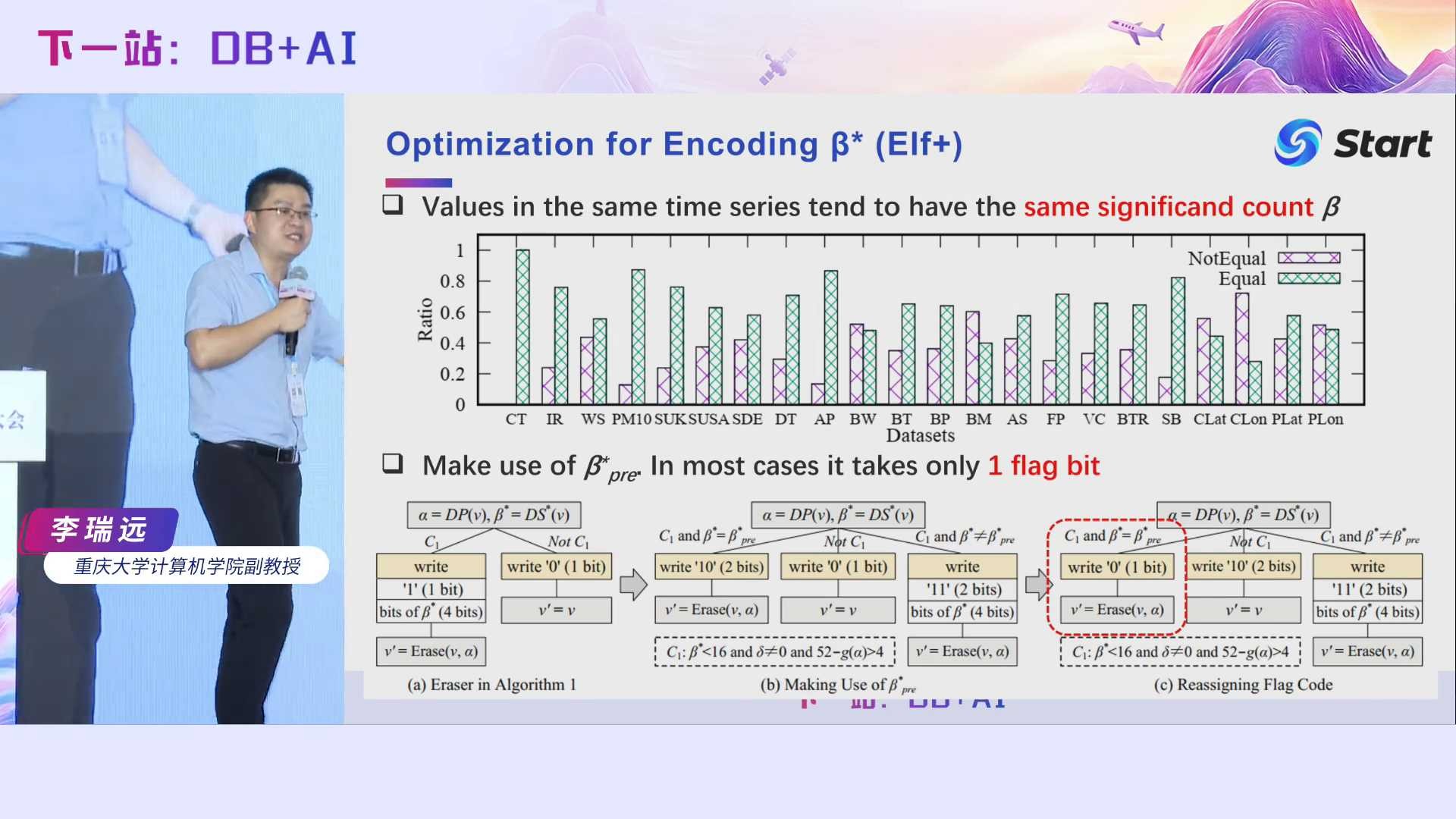
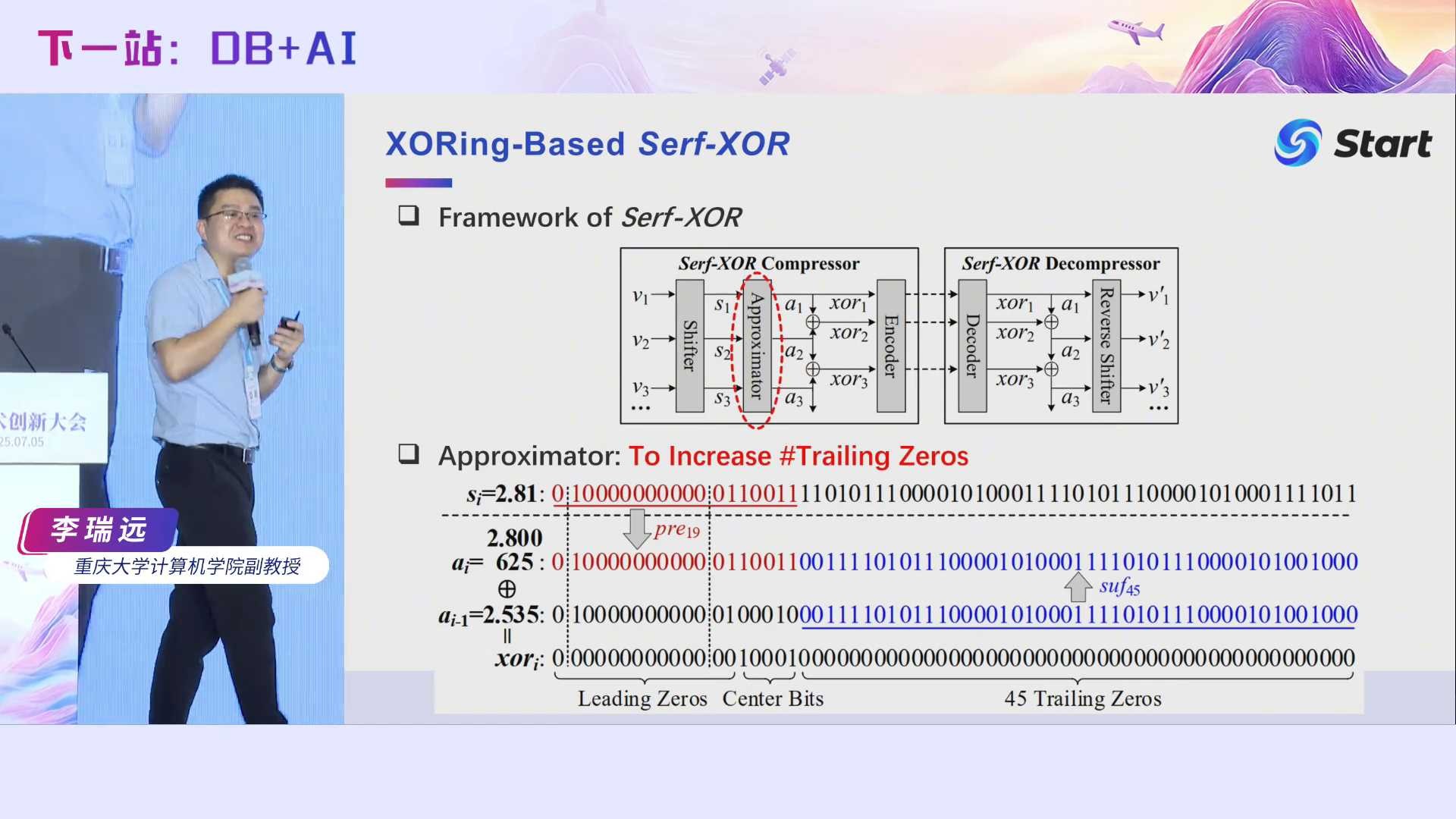
经过前面的步骤,我们可以得到同时拥有很多前导零和尾随零的异或值,接下来的话就是如何编码这些异或值。最简单的方法是,记录前导零的个数以及尾随零的个数,中间位我只要记录110101就行了,这样已经能够压得比较狠了,但是我们发现还有更狠的方法,我们借鉴了Gorilla的基本思想,并提出了一个近似规则的概念。具体而言,我们发现前导零个数分布极为不均,最多的前导零个数是64,最少的为0,但是他们大部分值都分布在7到31之间。近似规则其实是一个有序数组,比如我们选择的近似规则为有8个元素的有序数组[0, 8, 12, 16, 18, 22, 24]。近似规则怎么来用呢?如果我发现前导零个数是13,它落在12和16之间,那么我就认为它前导零个数只有12。这样做的好处是,如果我们原封不动地记录前导零的个数,它有可能有64种状态,需要8个字节记录它,是吧?但如果我们控制状态个数,即前面给出的近似规则只有8个状态,那么每个状态可以只用3个比特来表示,因为2的3次方是8。近似规则会引入一些额外开销,这个开销我们后面还会继续说。在VLDB 2023这个工作里面,我们根据数据分布,手动指定了一个近似规则,后面我们还会对它进一步优化。近似规则的引入,能够一定程度上提升我们的压缩率。
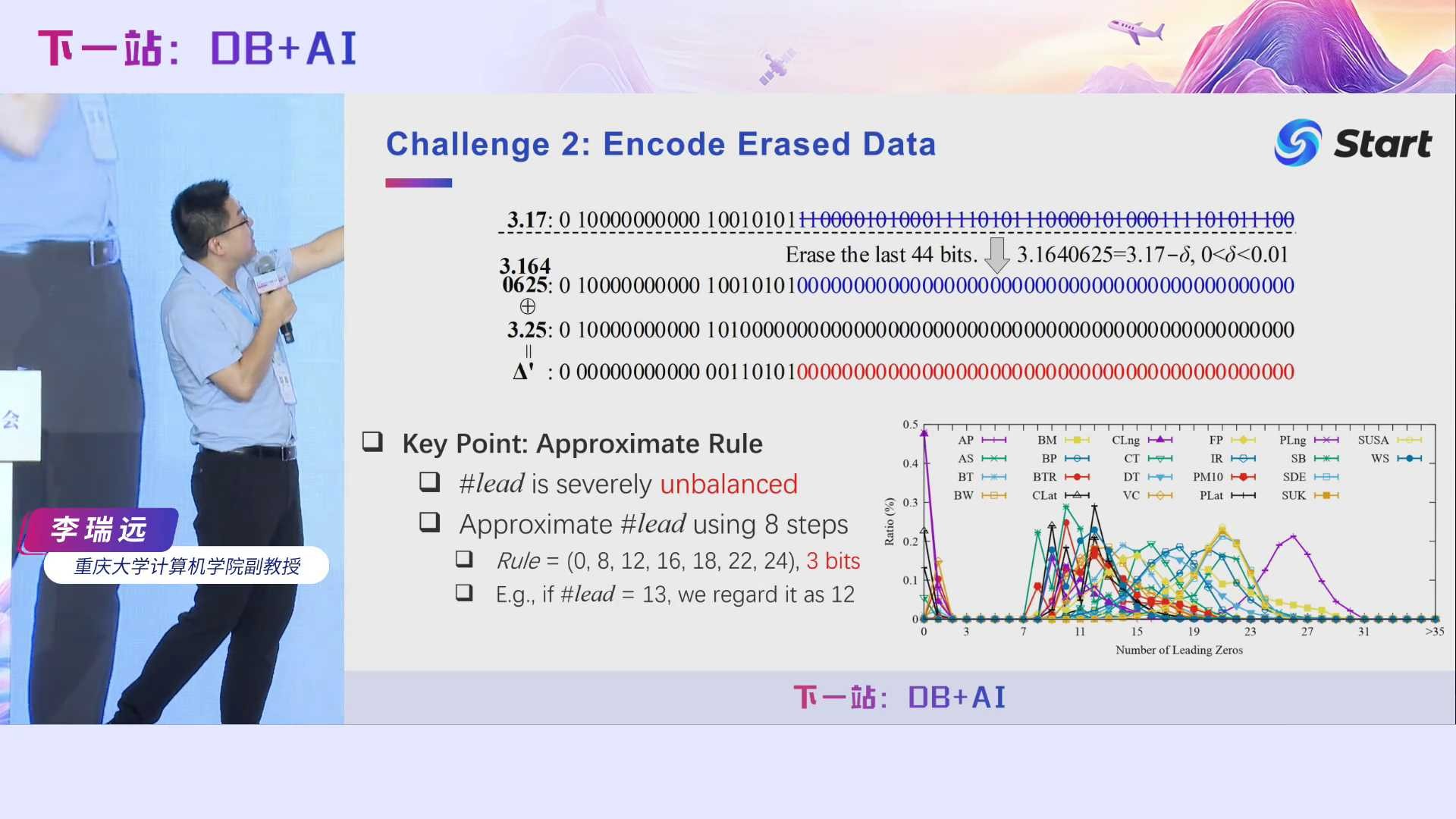
回到我们前面的第三个问题,即我们如何恢复原始的那个值呢?前面说了,为了恢复原来的值,我们需要知道它的精度。如果我们存储精度信息的话,由于计算机里面可表示的double类型绝对值最小的那个数大约为4.9*10^-324,也就是说double类型精度的最大值是324,这需要我们用9个比特来存储,这会非常耗空间,无法达到压缩的效果。那我们该怎么办呢?我们发现,我们不记录浮点数的精度值也可以完整恢复原来的值。我们只需要用4比特记录它的有效位数。什么叫有效位数?这也是我们初中学的一个知识。

我们简单地回顾一下有效位的定义。3.17的有效位是3, -0.0317的有效位还是3,也就是说,计算有效位时,我们不需要计算十进制数中前面的0,只要从左往右找第一个非零数字,然后再往后数有多少个数字即可。我们发现在压缩时其实只要记录浮点数的有效位β,通过β可以计算出我们需要的精度α。在计算机里面double类型的有效位最多为17到18,远远小于精度,因此所需的比特数更少。我们可以根据这个公式利用β来计算α。另外,我们证明,浮点数可擦除的位数只与β大小相关,其可擦除的位数可以通过这个公式计算出来。也就是说,当β大于等于16时,可擦除的位数小于4。为此,当β大于等于16时,我们不作擦除。也就是说,当擦除时,β只有16种状态,可以用4个比特表示即可。通过β求α,通过α来恢复我们的原来的值,这就是我们的大体思想。

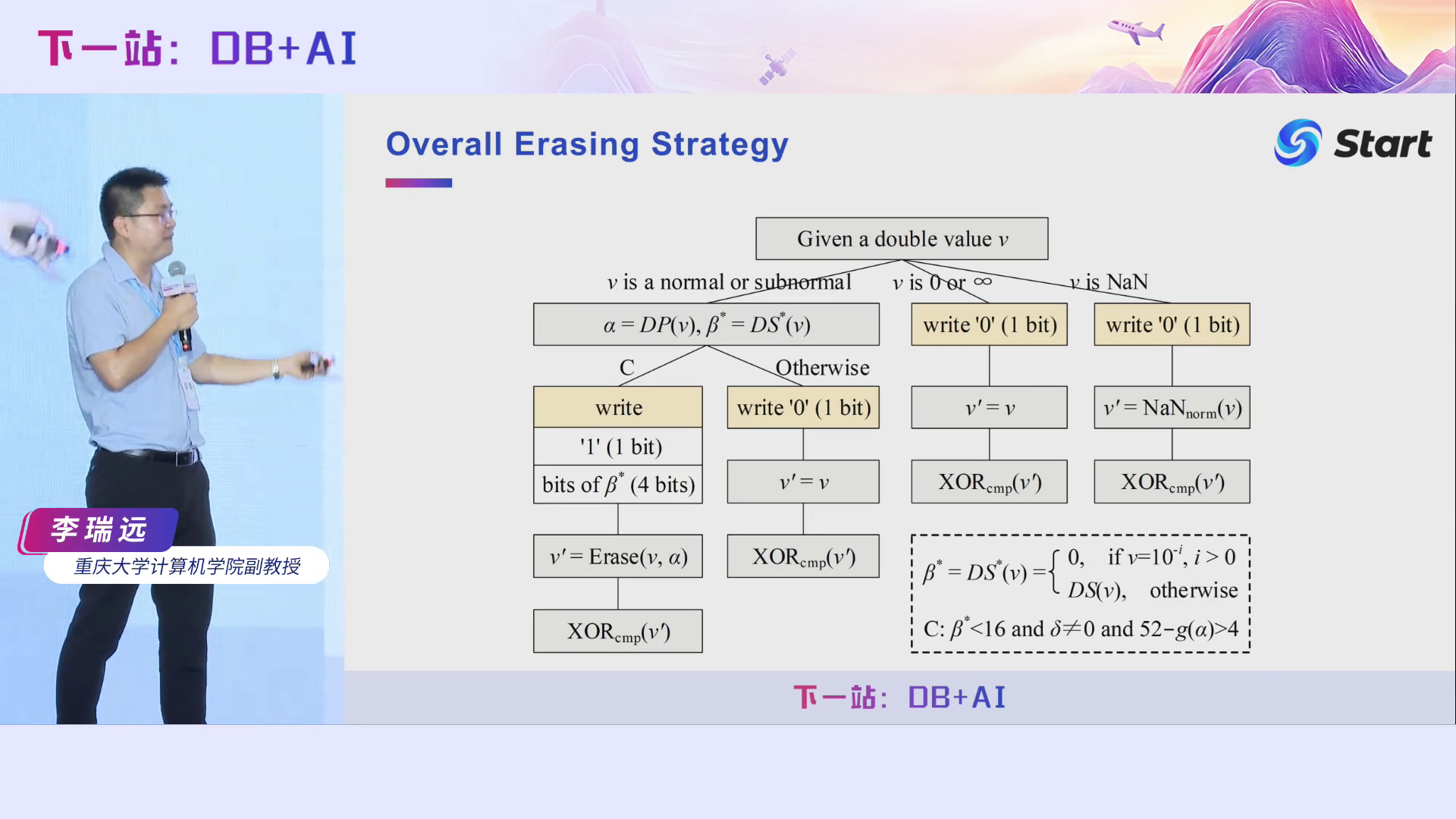
前面介绍的只是通用的浮点数(即正常数和零),而我们说过,浮点数有很多类型的。对于其他的浮点数据类型,以及一些Corner Case,论文中也做了一些讨论。

这是我们整个Elf算法的编码策略,看起来很复杂,其实逻辑比较简单,就像决策树一样,给定一个浮点数据,根据不同的情况走不同的分支即可。
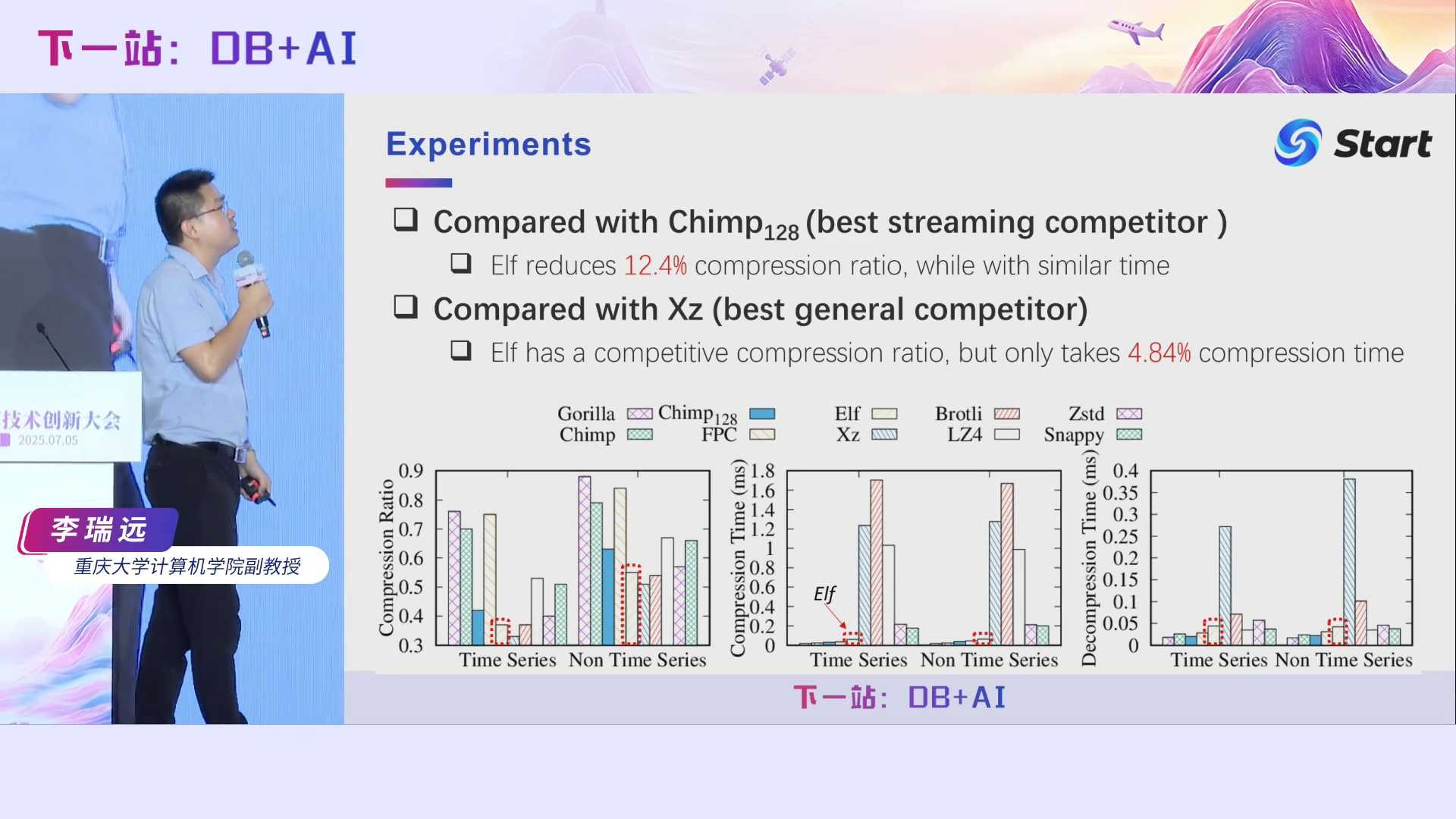
我们采用了多个数据集进行了大量的实验。相对于当时最好的对比方法Chimp128,我们Elf能够减少12.4%的压缩率。注意我们这里的压缩率是压缩后的数据大小比上压缩前的数据大小,所以就是越小越好。而且我们与通用压缩算法Xz相比,压缩率相当。Xz应该是压缩得非常狠的一种压缩格式了,但是它非常慢。Elf的压缩率虽然跟它差不多,但是我们的压缩时间仅是它们的4.84%。
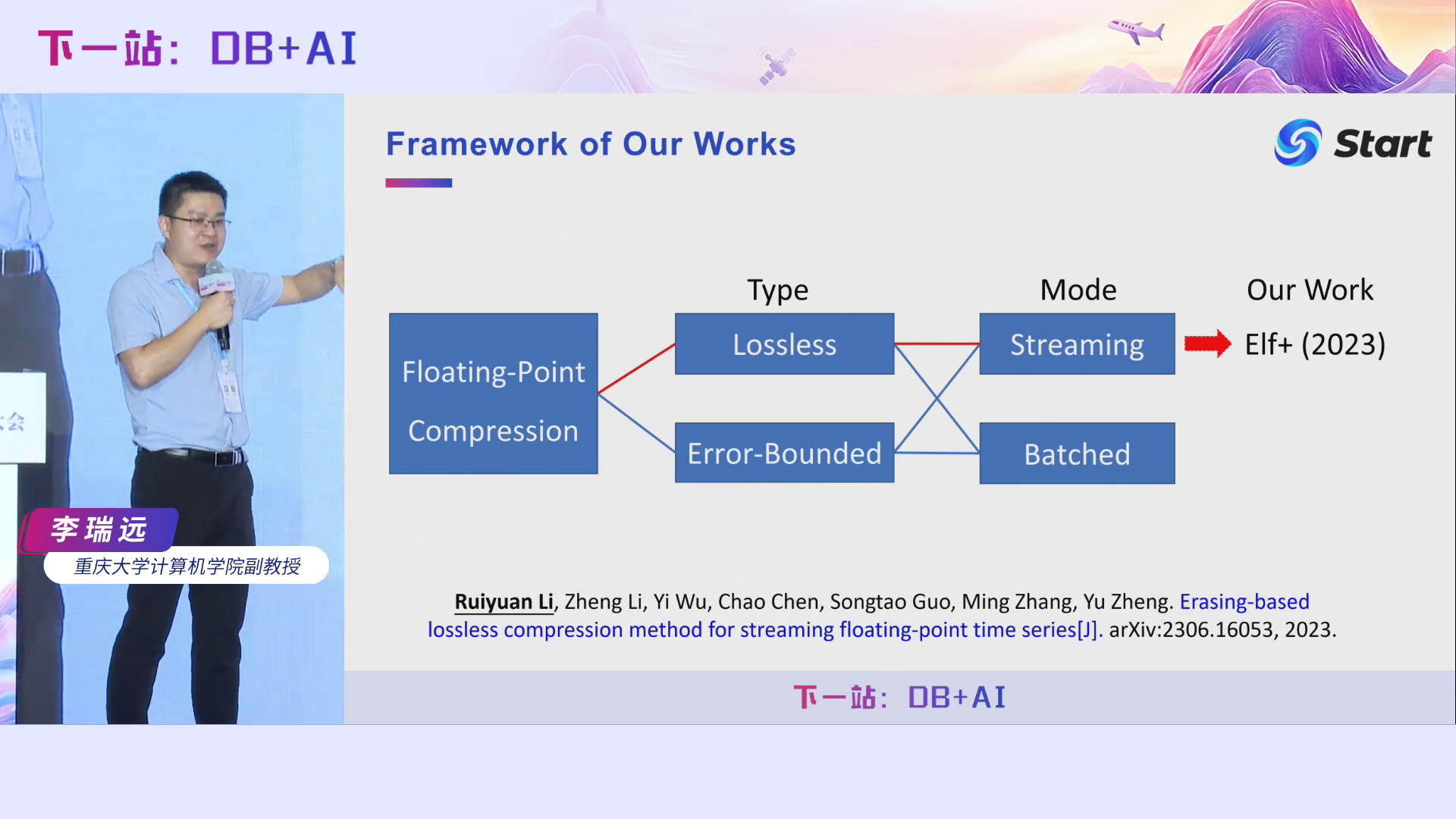
Elf这篇文章我们第一次投VLDB直接就被Accept了。接下来要介绍的第二篇工作是Elf文章的一个升级版,我们称之为Elf+。称之为升级版是因为它的核心Contribution其实不是很大,所以我只是直接放到arXiv上了,作为了Elf的补充。
让我们回顾一下Elf的编码策略,我们发现存储有效位β花了4个比特位和1个标记位来记录,即共花了5个比特位。但是有必要花这么多比特来记录有效位β吗?其实没必要。

我们发现在一个时序数据集里面,同一个时序值的有效位数是差不多的。比如说温度一般保留到一位小数就行,例如今天北京天气是37.5度,温度大多数情况有效位就是3,即有效位数其实变化不大。我们也做了一些统计,对于同一个时序数据,我们检查某个值跟它前一个值的有效位数是否相同,这里绿色的柱子表示相同的比例,红色的柱子表示不相同的比例。我们可以看到,大部分都是相同的。因此,我们其实没必要花4~5个比特来记录每一个数的有效位了。我们可以采用一个标记位,如果当前数的有效位与前一个数的有效位相同,我们只需要用一个比特来存储就行了。
另外,给定一个浮点数,它的有效位数计算其实是非常难的。我们现场很多人应该都是编程人员。大家可以想想,在Java语言中,如果给你一个浮点数,你怎么能够得到它的有效位?最简单的想法就是把它转换成一个字符串,然后再数就行了是吧?但是数据转换过程相对于压缩任务本身而言是非常慢的。Java提供的BigDecimal因为实现了很多更复杂的逻辑,因此效率更慢。
那怎么办呢?我们提出了一个近似的解法,虽然可能会多数一些,但是不影响我们无损压缩的正确性。怎么个近似法呢?我们采用了一种“试错法”,不断地判断这个公式是否正确,即v乘以10的i次方是否等于v乘10的i方后下取整?如果相等,我们就认为已经得到了精度α,然后再通过α计算出β。当然这可能存在一些误差。我们做了很多实验,所求的精度只会比真实的要大而不会小。所以我们大不了少擦除一些位,多记录一点点,压缩率损失一点点,但是不会影响我们压缩解压的正确性。
我们还可以利用同一个时序数据集中数据具有相同有效位的特性,进一步加速有效位的计算效率。前面“试错法”的判断中,直观的做法是从0开始枚举i,但这有可能枚举多次才能计算出结果。我们可以从前一个数的β所对应的i值开始枚举,平均判断次数仅为一次,大大提升了效率。
通过我们的优化, Elf+相对于第一个版本Elf,压缩率进一步降低了7.6%,而压缩时间降低了20%左右。

第三个工作也是Elf的改进版本,既有流式的方法,也有批式的方法,最近被IoTJ接收了。
这个工作要解决其实就是编码问题。让我们回顾一下Elf+的编码,我们发现它有很多不足的地方,比如:它分开编码标记位和有效位,并没有捕捉它们的联系;它手动地指定近似规则,对于不同的数据可能不是最优的;它花了高达5位或者7位的比特来记录中心位的个数,非常耗费空间;是否与前一个值共用一些信息(比如β值)的判定也不是最优的。针对这些问题,我们这篇工作分别做了优化。接下来我们重点介绍针对近似规则的优化。其他的优化大家可以看我们的原文。

近似规则,还记得吧?我在Elf里面,手动地指定了一个近似规则,它是一个有序数组:ruleelf= [0, 8, 12, 16, 18, 20, 22, 24]。如果前导零个数为13时,我们认为它为12,因为它落在了12和16之间。但这里会带来一个误差,即本来一个比特是属于前导零的,但我们误认为它属于中心位,因此不得不原生存储它,我们称之为近似开销。另外,存储近似规则的每个状态也需要一些开销,例如Elf的近似规则有8个状态,我们可以用3个比特来表示,3就是这个近似规则的表示开销。近似开销和表示开销是此消彼长的,我们希望找到一个近似规则,使得近似开销和表示开销总和最少。即我们把我们的压缩问题,转化成了一个查询问题。

如何找到最优的近似规则呢?这个其实也是一个排列组合的问题,非常复杂。我们主要是提出了一个动态规划思想,并且提出了很多的pruning的策略,使得查找时间尽可能少。

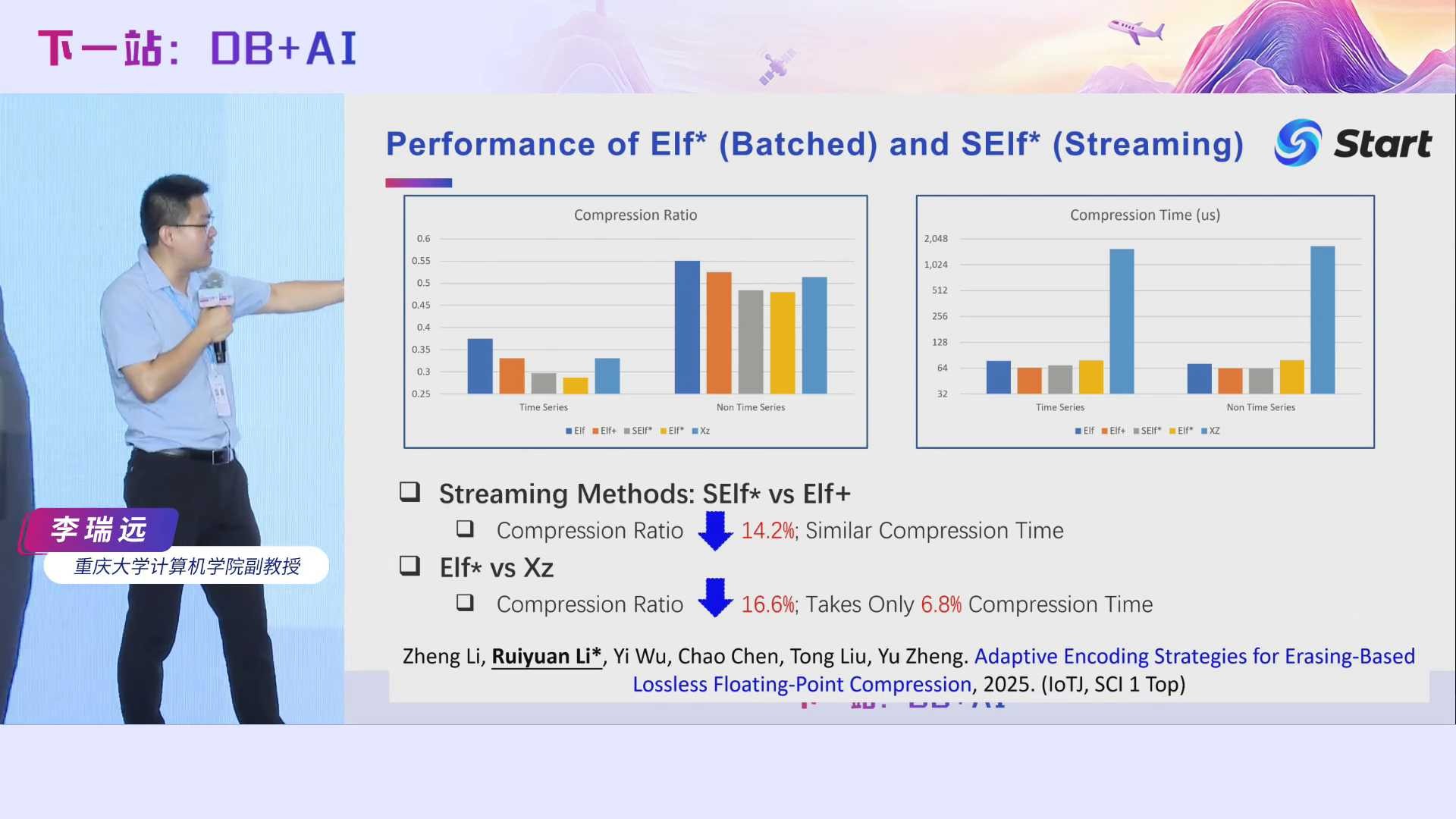
由于我们需要计算近似规则,因此Elf*相对于之前的Elf+压缩时间有一些增加,但是通过我们的多种优化,它的压缩效率跟Elf+的差不多了。需要注意的是,它的压缩率相对于Elf+进一步下降了14.2%。相对于Xz,它的压缩率下降得更多,达到了16.6%,而它的时间只花费了Xz的6.8%。
最后一个工作是Serf。前面我们介绍的方法都是无损的,Serf是有损流式压缩算法。

Serf主要是面向于流式传输的场景。我们可以设想一下,我们有一组IoT的设备,IoT设备的计算资源和存储资源通常非常有限。在IoT设备中有一些传感器,传感器本身有一些测量误差。传感器不断地收集数据,通过无线网络传输到服务器中。IoT设备与服务器之前的带宽非常有限。用得比较多的IoT传输协议是Zigbee,它的网络带宽是非常低的,其理论带宽仅为20至250k比特每秒,这还仅仅是一个理论带宽,而实际带宽比这个要小得多。此外,服务器希望能够尽快地接收到传感器的数据,并对这些数据进行实时分析。实时分析在很多场景也非常重要, 比如说我们打车,高德打车,你打的出租车明明在你旁边了,但是如果有很大延迟,你手机里显示出租车还在很远的位置,你的体验就非常不好,是吧?因此,我们希望数据能够尽快传输到服务端来。假如我们GPS点的采样频率是1秒1个点,这已经很高了。如果要等10个点收集完之后再压缩传输,即使忽略传输时间,那么延时也要10秒钟,这也是不可忍受的,批式压缩通常会带来很大的延迟,不适合我们这个场景。在我们这个场景里面,我们希望收到一条记录后,立即压缩并传出去,这就是我们流式压缩的概念。另一方面,很多场景其实不需要精确的数据,比如我们刚刚打车的例子,GPS点本身可能有5~10米的误差,通过压缩叠加几厘米的误差,对上层应用来说几乎没有什么影响。Error-Bounded的有损压缩算法能够极大提高压缩率,减少带宽占用,也能减少我们流量费的使用,这些对用户来说都是实实在在的好处。我们做了一个调研,发现当前已经有很多批式无损压缩算法,还有很多流式无损压缩算法,也有很多批式有损压缩算法,但是流式有损压缩算法几乎没有。为此,我们以这个作为切入点,设计了Serf算法,并发表在了今年的SIGMOD会议上。

流式有损压缩的挑战是什么呢?首先我们要保证流式压缩,就无法利用数据的一些共有特性,即在流式场景里面,要保持一个很好的压缩率是非常困难的。其次就是效率问题,由于IoT设备的计算资源非常有限,如何利用这些有限的资源保证压缩效率也是非常困难的。为此,我们提出了一个高效的流式有损压缩方法Serf,它也是英文方法名的首字母缩写。Serf主要有两种方法,一种是基于量化的,另一种是基于异或的。基于异或的方法是我们这篇文章的主要贡献,因此,接下来我主要讲的是基于异或的方法。

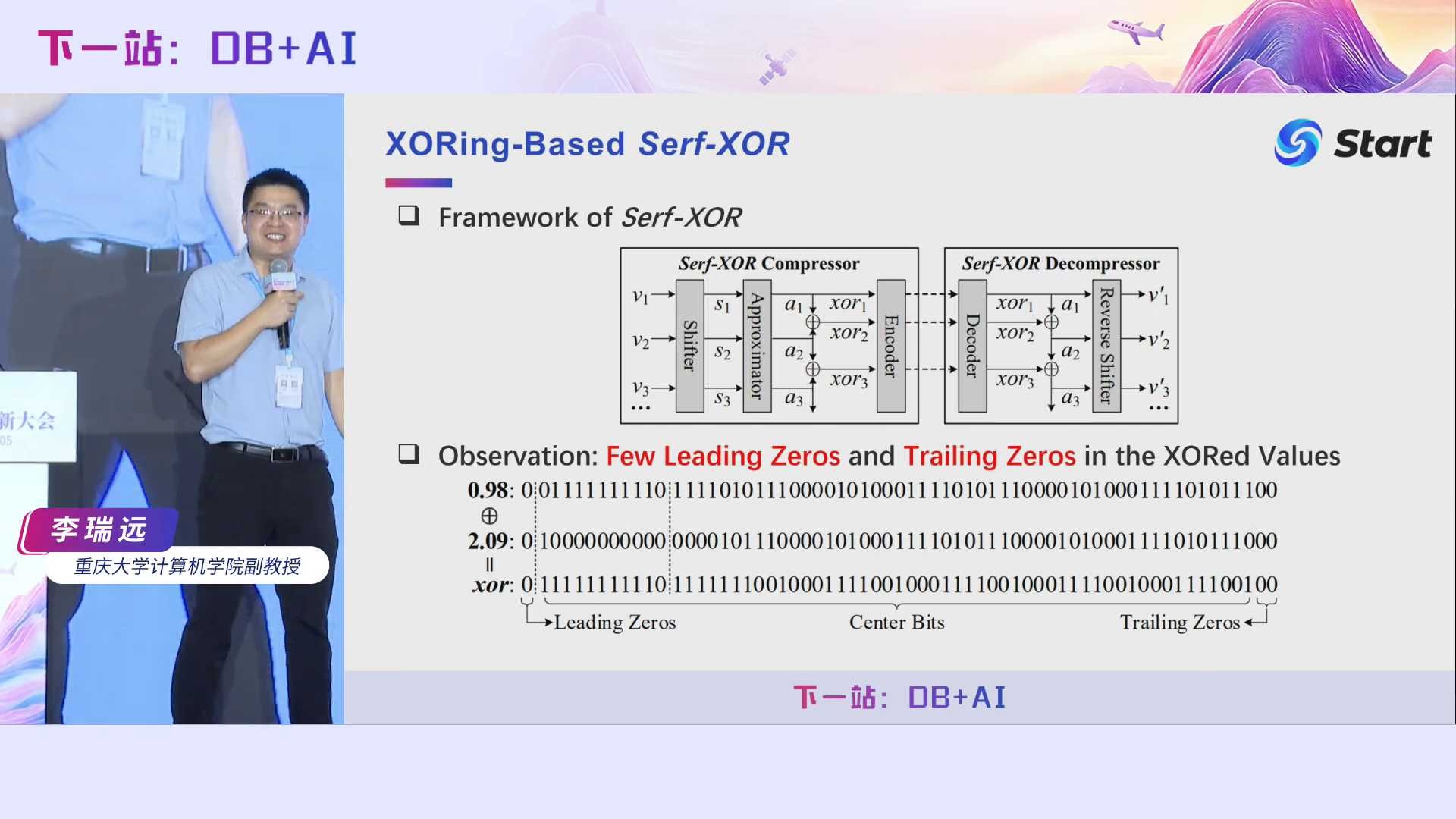
让我们看看现有基于异或操作的方法可能有什么问题。给定两个浮点数0.98和2.09,它们进行异或操作,得到的异或值长这样,我们可以看到它只有1个前导零和2个尾随零,因此对它的压缩效果不会很好。即使利用我们前面Elf的方法对0.98和2.09进行擦除操作,能够增加尾随零,但是Elf是面向无损压缩的,在允许误差有界的情况下,它的压缩率还可以进一步提高。我们Serf主要解决的就是两件事情,第一,如何增加前导零。第二,如何增加尾随零。
我们首先看看如何增加前导零。什么情况下,前导零会非常少呢?第一种情况,当相邻两个数的符号不同时,它们之间的异或结果不包含任何前导零,这是比较容易理解的。另一种情况,当相邻两个数的值跨过了2的n次方时,他们的前导零也会非常少。例如我们前面给的例子,0.98和2.09跨了2的1次方,导致他们的指数位完全不同,进而造成了它们之间异或值的前导零只有1个。所以,要增加前导零,基本想法就是让它们的指数位相同。为此,我们提出了一种算法,称之为数据偏移,给每个数都加上一个数,使得所有数的符号位和指数位完全相同,在解压的时候,只需要减去这个数即可。但具体加上多大的数呢?我们理论证明,只需要加上这么一个数,我们就可以保证前导零非常多了,再更大的数只会让压缩率降低。这里给出了一个例子,假如原始的值是-0.96和2.02,它们的异或值没有前导零。我们给它们都加上5,得到4.04和7.02。对它们进行异或操作后,前导零变成了12个。
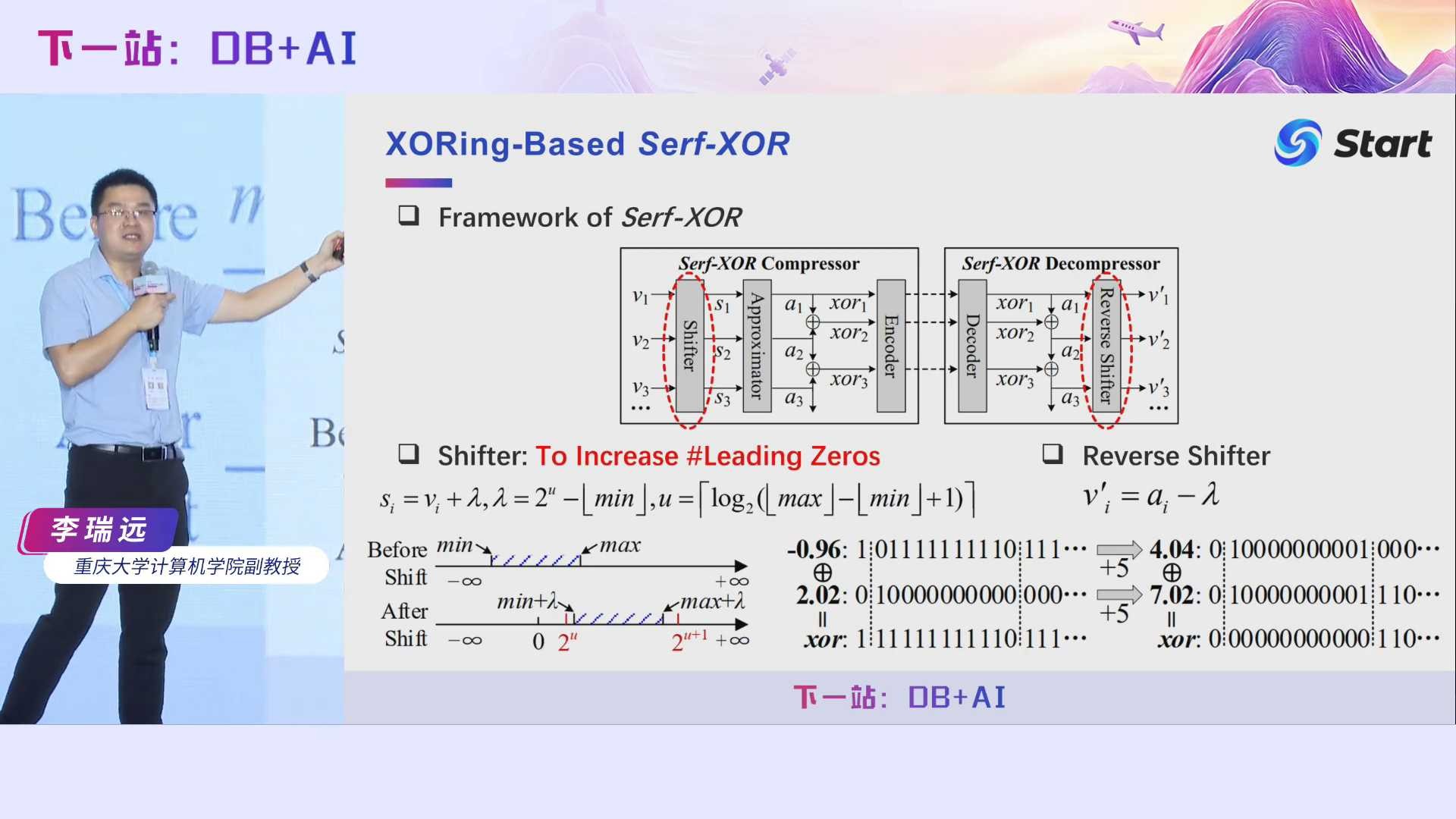
接着我们看看如何增加尾随零,主要通过近似器来实现。它的思想也非常简单,假设si是当前偏移后的值,ai-1是上一个偏移值的近似值,我们只需要将si的前几位和ai-1的后几位进行拼接,得到ai,那么ai与ai-1的异或值肯定会有很多尾随零。到底用si的前多少位和ai-1的后多少位进行拼接,我们论文中也做了一些讨论和优化,并进一步提高了效率。有了前导零和尾随零都很多的异或值后,我们就用Elf*提出的编码进行压缩即可。
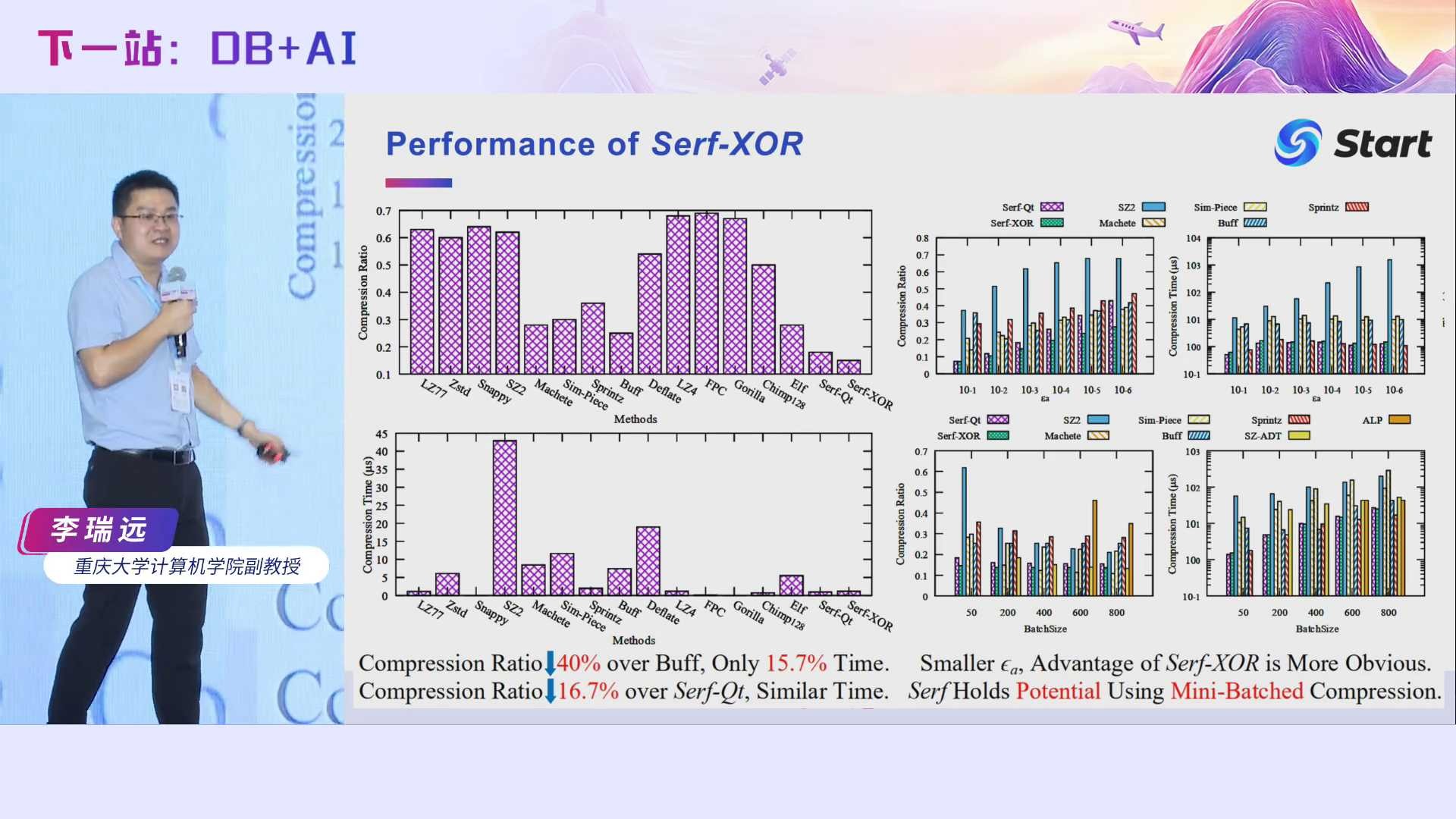
相对于当时最好的对比方法Buff,Serf的压缩率降低了40%,但是时间只花了它的15.7%。
由于时间有限,今天我只讲了一些大体思想,很多细节都没有讲到,如果感兴趣的话,可以去看我们的原文,我把所有的论文都列在这里了。

此外,我们也开源了所有的代码,大家可以关注我们实验室的公众号“时空实验室”,回复“时序压缩202504”,可以获得所有论文的pdf、详细解析以及源代码。谢谢大家!


关注公众号,回复“IoTDB时序压缩”,获得本次演讲PPT

0 条评论