康瑞部落

随着定位技术的发展以及IOT设备的普及，大量的轨迹数据可以被采集分析。轨迹数据一般被表示成位置与其采集时间的序列。了解轨迹之间的相似度，有非常多的应用，例如：密切接触者追踪，伴侣检测，个性化推荐等。然而，实际应用中，轨迹中的位置信息往往是有噪声的；同时，不同轨迹的采样率有所不同，在某些场景中，轨迹的采样率甚至可能很低。这都为轨迹相似度的比较带来很大的挑战。

本文将介绍香港科技大学、台湾交通大学、台湾中兴大学发表在ICDE 2021上的论文《Spatial-Temporal Similarityfor Trajectories with Location Noise and Sporadic Sampling》。该论文提出了一种高效的时空相似度比较方法，通过估计用户在不同时刻位置的概率分布，进而推测不同用户在不同时刻处于相同位置的概率，并以此作为两条轨迹的时空相似度。

一、问题背景

近年来，IoT设备与定位技术得到快速的发展，物体（用户或者其设备）的位置可以通过各种不同信号进行获取，例如GPS，WiFi，蓝牙等；另外，当用户使用各种日常服务时，也在不同的系统中留下了自己的位置信息，例如移动支付（微信、支付宝和信用卡）；公共运输系统的刷卡记录；电信服务时的基站连接；共享单车与网约车服务。因此，如今的不同系统收集了大量包含位置与时间的用户轨迹数据（trajectory）。用户的轨迹通常表示成一些离散的位置及其对应的时间戳，可以被看作是从一条连续的路径（continuous path）中采样得到的。

如果我们把地理空间网格化，当两条路径某个相同的时刻处于相同的格子中时，我们就认为两条路径有一个共享位置（co-location）。本文中，轨迹时空相似度就是用来衡量两条路径co-location的程度，即它们在时间与空间维度重合的情况。

衡量轨迹的时空相似度有着许多非常重要的应用。诚如前文所言，用户在不同的系统中都留下了自己的轨迹，这些轨迹都可以看成是从用户日常的路径采样得到的，通过比较轨迹的时空相似度，我们可以将不同系统中属于相同用户的轨迹进行匹配，从而实现更全面的用户分析。另外，通过比较不同用户轨迹的时空相似度，我们可以了解用户之间的关系，更好地服务于诸如商品推荐、个性化营销等不同的应用。

然而，因为位置噪声与间断采样的影响，衡量轨迹时空相似度仍然是一个具有挑战的工作。

• 位置噪声（location noise）：轨迹中的定位结果往往是充满噪声的。因此，处于相同位置的两个用户的定位结果可能相距甚远(图一(a))；反之亦然。因为位置噪声的存在，直接比较轨迹中位置的距离来衡量轨迹相似度并不可行。

• 间断采样（sporadic sampling）：由于轨迹中的位置是间断性地从用户行走的路径中采样得到的，并且不同用户的采样频率不尽相同，因此，用户的实际位置并不总是能从轨迹数据中观察到。如图一(b)所示，同时沿着相同路径走的两个用户，即使不考虑位置噪声的影响，因为两者采样率不同，其轨迹中的位置可能完全不存在重合的部分。因此，直接通过比较轨迹中位置的距离来衡量轨迹时空相似度会严重受间断采样的影响。更有甚者，轨迹的采样频率在某些场景（例如，CDR 数据， 移动支付数据， 公共运输系统数据）下可能非常低，这给相似度的比较带来个更大的挑战。

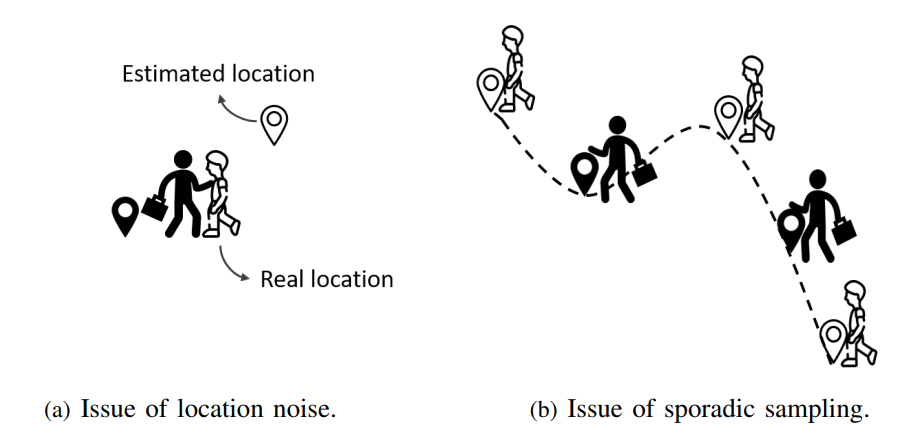
图1 轨迹相似度比较的困难与挑战

针对以上提及的困难与挑战，本文主要通过以下几个方面进行解决：（1）首先，为减少位置噪声的影响，本文将轨迹中的位置看成是一个位置概率分布，而不是空间中一个确定的点；（2）其次，为解决间断采样的问题，根据用户的轨迹数据，本文利用个性化的速度模型推测出该用户在任意给定时刻的位置概率分布；（3）最后，基于以上推算的概率分布，本文利用两条轨迹在不同时刻平均的co-location概率来表示两条轨迹的时空相似度。

二、模型结构

为解决位置噪声与间断采样影响下的轨迹时空相似度度量，本文提出了一个新的算法STS，图二展示了其基本的结构：给定两条带有噪声的轨迹，STS首先分别为每条轨迹计算出任意给定时刻的位置概率分布（spatial-temporal probability）；根据计算得到的时空概率，STS进一步计算得到两条轨迹同时处在相同位置的概率（co-location probability），并基于此得到两条轨迹的时空相似度。下文将对每个部分逐一展开介绍。

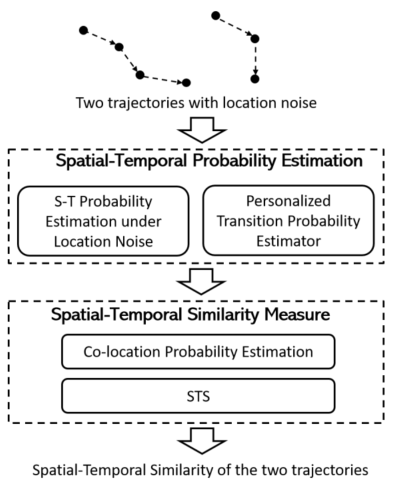
图2 STS算法的基本结构

1、噪声影响下的时空概率计算

首先，我们把地理空间切分成n个网格，用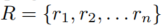表示。接着，给定一条轨迹Tra, 本文进一步推导出物体在时间t时刻处于某个网格的概率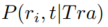。根据条件概率的定义，该概率可以表示成

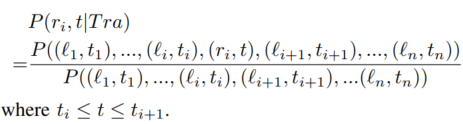
同时，本文假设用户在不同位置的迁移具有马尔可夫属性，即用户当前的位置只与用户上一个时刻的位置有关。因此，上述公式可进一步推导为：

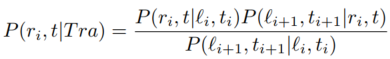
此处，与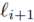都是原轨迹中的带有噪声的位置，因此本文进一步将其表示成一个概率分布。本文用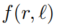表示当给定轨迹中某个位置，用户实际的位置在的概率，因此，当考虑位置噪声的存在时，上述公式可以进一步表示为

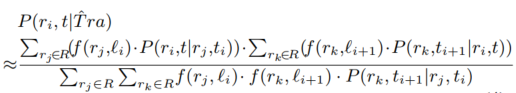
    综上，物体在任意时刻位于任意网格内的概率可以如下计算：

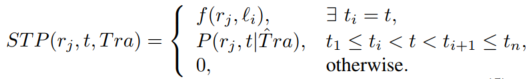
 2、迁移概率

上述式子中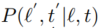，表示物体在时间间隔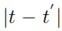中从迁移到的概率。因此，本文提出利用物体速度的概率来表示物体在不同位置之间迁移的概率。考虑到不同物体的速度概率分布不同，本文提出了一个基于核密度估计的方法来个性化地计算物体的速度概率分布，并借此来表示物体的迁移概率。给定任意一条轨迹，核密度估计法包含两个步骤：1.首先，计算轨迹中任意两个相邻的位置的速度，得到物体速度的序列；2. 接着，基于速度的序列，本文利用以下公式对核密度进行估计：

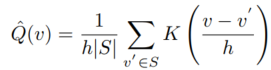
其中，S表示的是速度的序列，K()表示核函数（本文使用了广泛应用的高斯核函数），h>0表示带宽。于是，物体速度的概率就可以表示为：

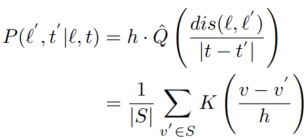
3、Co-location概率计算

基于上述概率的推导与计算，给定两条轨迹Tra₁与Tra₂，它们在时间t时刻同时位于网格r的概率可以表示为他们时刻t位于r的时空概率的乘积：

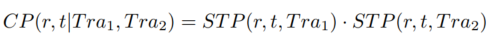
因此，与在t时刻co-location的概率为：

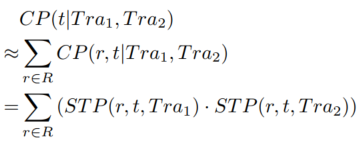
4、时空概率

给定两条轨迹Tra₁与Tra₂，本文用两条轨迹在所有时间戳的co-location概率的平均值来表示他们的时空相似度。

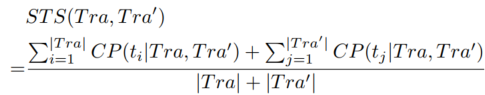
三、实验结果

本文利用一个室外的出租车轨迹数据集以及一个室内的行人轨迹数据集进行了实验，着重比较了STS与其他相似度方法在轨迹匹配（trajectory matching）的任务上的表现。对于数据集中的一条轨迹，本文首先通过间隔采样将其分成两条子轨迹，分配到两个子数据集中。因为这两条子轨迹来自同一条轨迹，相比较于其他的子轨迹，其时空相似度更大。本文定义了准确率与平均排名对实验效果进行量化的分析。高准确率与低平均排名表示方法具有更好的效果。

文中主要讨论了低采样率、不同采样率以及位置噪声对时空相似度比较的影响，图三到图五呈现了STS与其他算法在出租车数据集上的比较结果。从图中可以看出，在不同的情形下，本文提出的STS方法相较于其他方法都有更高的准确率跟更低的平均排名，说明本文提出的方法能够更好地解决低采样率、不同采样率以及位置噪声的影响。

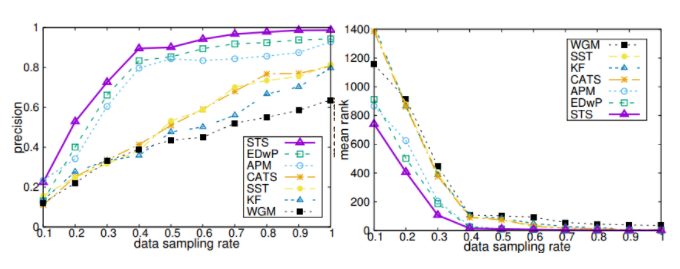
图3 低采样率的影响

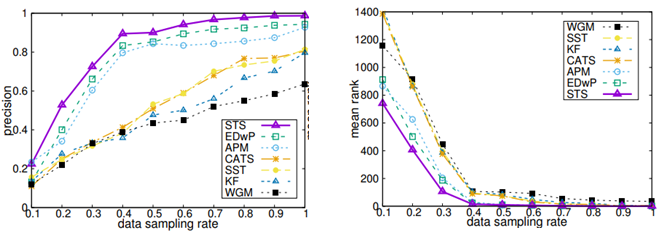
图4 不同采样率的影响

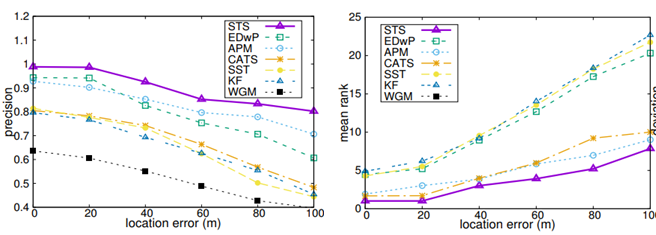
图5 位置噪声的影响

四、小结

针对轨迹中位置噪声以及间断采样的影响，本文提出了一个比较轨迹时空相似度的方法。首先，通过将轨迹中的位置表示成空间中概率分布，并估计物体在任意时刻的位置概率分布；接着，本文进一步计算两条轨迹同时位于相同网格的概率（co-location概率）。基于此，本文使用两条轨迹在不同时刻的平均co-location概率来表示两条轨迹的时空相似度。本文利用室外的出租车数据与室内的行人数据对方法的有效性进行了验证，并与其他方法进行了比较。实验结果表明，本文提出的方法在位置噪声以及间断采样的影响下，比其他现有的方法能更好地比较轨迹之间的时空相似度。

JUST持续为您分享时空数据前沿成果，也欢迎读者积极投稿。

关注公众号，回复“ICDE2021STS”，下载论文