分类:
时空数据
|
浏览 (3647)
|
评论 ()
一、空间连接定义 随着全球定位系统和移动互联设备的普及,海量的空间数据也随之产生。空间连接(Spatial Join)运算是一类最常用的空间数据分析算子,具有广泛的应用场景。例如统计地铁站周围500米的POI,帮助店主合理选择商铺选址;从同一个数据集中分析空间相邻的同伴关系,辅助警方侦察;查询河流周围的居民区和农田,在汛期排除洪水隐患;查找去过疫区的人群,方便疫情防控等。 下面给出空间连接的定义:给定空间对相集合R和S以及空间谓词 θ ,计算并输出所有空间对象二元组( r , s ),满足 r ∈R, s ∈S,且 r 和 s 满足空间谓词 θ ,形式化定义如下。
空间谓词θ 可以分为三类。 1)空间拓扑:如 intersects (相交)、 contains (包含)等; 2)空间距离:即 distance ,表示空间对象 s 与 r 的空间距离小于等于设定阈值 δ ,由定义(1)派生出 distance 连接的定义如下。 (2)
3)空间 k 最近邻:即 kNN (k Nearest Neighbors),表示空间对象 s 是数据集S中与 r 距离最近的 k 个空间对象之一,由定义(1)派生出 kNN 连接的定义如下。
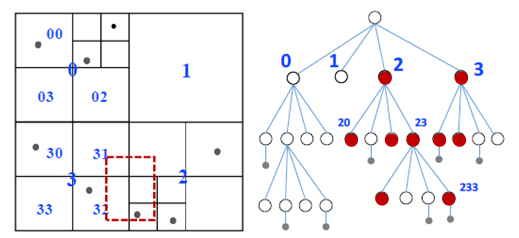
另外,空间对象可分为三种类型:点(Point)、线(LineString)、面(Polygon)。点是最简单的空间对象,线和面是复杂空间对象,其空间运算相对耗时。为了简化计算,一般用空间对象的最小边界矩形MBR(MinimumBounding Rectangle)进行空间运算,得到近似结果,然后对近似结果进一步提纯过滤,得到最终的精确解。 空间连接运算是基于空间索引实现的,空间索引能够通过快速过滤来提高查询效率,基于空间索引的空间连接的运算过程如下: 1)构建空间索引。对集合S中所有空间对象 s ,利用 s.mbr 构建空间索引 I 。 2)循环查询。对集合R中的每个空间对象 r , 用 r 查询索引 I 中与其满足空间谓词 θ 的所有空间对象 s ,并将二元组( r,s )加入结果集。 空间索引不止一种,选取合理的空间索引对提高空间连接运算的性能至关重要。为了验证空间索引对空间连接运算性能的影响,本文首先在第2节中介绍几种最常用的空间索引。然后在第3节进行实验对比,分别以空间索引、空间对象类型、空间连接谓词为变量,分析影响空间连接运算性能的因素。 空间索引一般是基于数据结构中的树来实现的。在索引树上,一个节点对应一个矩形的空间范围,父节点的空间范围包含所有子节点的空间范围。空间对象依据其MBR,存储在树的对应节点上。在查询时,首先依据查询对象的MBR遍历树上与该MBR相交的所有节点,并收集节点上存储的空间对象作为一个候选结果集,最后再根据空间谓词θ 做进一步过滤,保留满足空间谓词的候选对象,组成最终的结果集。下面分别介绍三种最常用的空间索引:Quadtree索引、KDtree索引和Rtree索引,且设定用数据集S构建索引,然后用数据集R中的空间对象r 查询空间索引。 Quadtree[1] 索引是一棵四叉树,支持所有空间对象类型。Quadtree将集合S的全局空间范围G 递归地划分成4子空间,直到子空间内的空间对象数量小于等于设定的阈值α ,并对四个子空间分别编号0、1、2、3,如图1(a)所示(α = 1)。然后用四叉树结构组织所有子空间,如图1(b)所示,树的根节点对应空间范围G ,一个节点对应一个子空间。对数据集S中的空间对象s ,将其存储在包含s .mbr 的最小子空间对应的节点中,当s 是空间点时,s 与s.mbr 空间上等价,所有空间点均存储在叶子节点中,如图1所示。
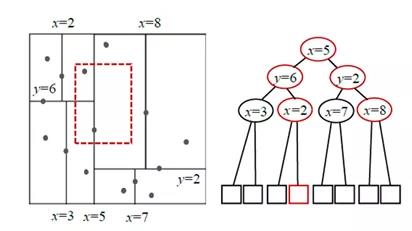
在查询时,使用 r.mbr 近似表示空间对象 r ,查找Quadtree中与 r . mbr 相交的节点,然后判断节点中的所有空间对象 s 是否与 r 存在空间相交关系。图1中,红色的矩形表示 r . mbr ,该矩形在Quadtree上遍历的节点标记为红色,然后找到叶子节点233上与其相交的一个空间点 s ,最后再判断 r 和 s 的相交关系。通过空间索引,可以快速过滤掉与查询框 r . mbr 不相交的节点,加快遍历查询效率。 KDtree[2] 索引是一棵二叉树,仅支持空间点对象。在构建索引时,首先使用集合S中第一个空间点s 1 的构建根节点root,根节点包含空间点s 1 和标签odd,odd是个布尔值,true表示该节点用s 1 .x 进行空间划分,false表示用s 1 .y ,KDtree中父节点和子节点的odd相反,即交替地使用x 和y 值进行空间划分。对于后续的空间点si (i>1),以root节点为当前节点,递归地执行以下步骤: 1)判断当前节点是否为叶子节点,若是执行步骤2),若不是执行步骤3); 2)设当前节点中存储的空间点是 s ,odd = true时根据 s.x 的值将当前节点对应的空间范围一分为二生成两个子节点,反之根据 s.y 的值进行划分。然后根据 si . x (或 si . y )与 s . x (或 s . y )的大小关系,将 si 保存到对应子节点上,子节点的odd值与当前节点相反; 3)利用步骤2)中描述的判断方法,得到子节点,并将其设为当前节点,然后执行步骤1)。
在构建好的KDtree索引中,每个空间点对应一个节点(叶子或非叶子节点),如图2所示。 查询时,用 r . mbr 遍历树上所有与之相交的节点,然后摘取节点上的空间点 s 并判断 r 与 s 是否空间相交。 在图2中,红色矩形表示 r . mbr ,它在KDtree上遍历的节点用红色标记。 Rtree [3] 索引是一棵多叉树,支持所有空间对象。Rtree构建索引的思想是空间聚类,对集合S中的所有空间对象聚类,生成 n 个聚类,然后自底向上递归地对 n 份聚类进一步执行聚类,直到 n = 1。Rtree中一个节点对应一个聚类,与Quadtree和KDtree不同的是,Rtree同一级别的节点之前可以存在重叠,这保证了一个空间对象仅属于一个Rtree的叶子节点,即Rtree中所有空间对象之存储在叶子节点中,如图3所示。
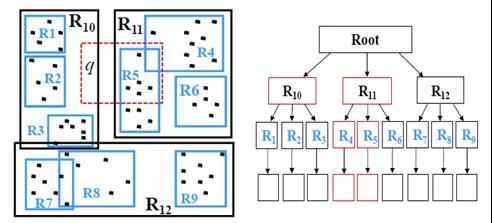
下面介绍一种JTS [5] (JavaTopology Suite)实现的一种Rtree索引——STRtree [4] 。该索引的构建步骤如下: 1)初始化集合C = { c 1 , c 2 , c 3 ,.., c n }, ci 是仅包含一个空间对象 si 的空间聚类, ci . mbr = si . mbr , n 是集合S中的空间对象数量。 2)STRtree有一个阈值 m ,表示一个非叶子节点所包含的最大子节点数量。γ = ⌈ n / m ⌉表示集合C需要被划分成 γ 个聚类。如果 γ = 1,说明 n ≤ m ,则将集合C聚类成一个根节点Root, ci 是Root的子节点,构建索引完成。如果 γ > 1,则执行步骤3)。 3) ε = ⌈sqrt( γ )⌉表示每个聚类在 x 和 y 方向上划分的份数。对集合C按照 ci . mbr . minx 在 x 方向递增排序,然后将其在 x 方向上平均地划分为 ε 份聚类,然后对每份结果在 y 方向上按照 ci . mbr . miny 排序并平均地划分成 ε 份聚类,两次划分生成大于等于 γ 份的聚类, γ ≤ k < n ,集合C中的聚类是集合C’中聚类的子节点。用C’替换C,然后执行步骤2)。 在查询时,同样用 r . mbr 遍历STRtree中与之相交的节点,并收集叶子节点上存储的所有空间对象 s ,然后判断 r 和 s 是否空间相交。遍历过程如图3中红色节点所示。 三、实验分析 为了验证不同空间索引在空间连接运算中的性能,我们利用真实的空间数据对不同空间索引、不同空间对象类型和不同空间连接运算做了对比实验,总结出了不同空间索引的适用场景。 3.1 实验数据和实验环境 我们使用OSM(Open Street Map)提供的部分全球空间数据作为实验数据,如表1所示。实验环境是8核CPU、16GB内存的个人电脑。 表1 实验数据集 数据集 点(Point) 线(LineString) 面(Polygon) 数据量 50万条 20万条 20万条 文件大小 5.47MB 62.1MB 57.5MB
3.2 实验结果 实验的变量有三种:空间索引、空间对象类型、空间连接运算。统计的实验数据有空间索引的构建时长和空间连接的运算时长。另外,实验中调用的空间索引都是JTS [5] 实现的。 图4展示了构建空间索引的耗时情况。取STRtree的阈值 m = 10,从图中可看出,不管对于哪种空间对象类型,构建STRtree索引的耗时最短,因为STRtree每个节点的子节点数量最大,所以节点数量最少,树的深度最小,则构建索引时的递归层数也最小。KDtree索引仅支持空间点,由于是二叉树,且每个节点仅存储一个空间点,KDtree的节点个数最多,树的深度最深,因此其构建时间最长。Quadtree是四叉树,其构建索引时间介于KDtree和STRtree之间,且远大于STRtree。
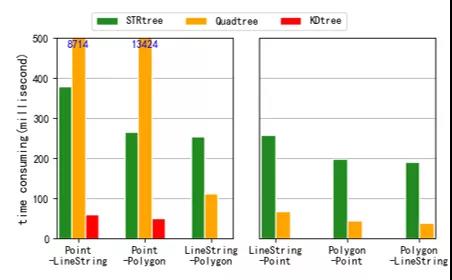
图4 空间索引的构建性能 图5展示了空间拓扑连接的实验性能,谓词 θ = intersects 。图中 x 轴下标的格式为S-R,例如Point-LineString表示对Point数据集构建空间索引,然后用LineString数据集中的空间对象查询空间索引。对空间点构建Quadtree索引,用数据集LineString和Polygon去查询时,计算耗时非常长,分别达到了8714毫秒和13424毫秒,说明Quadtree索引并不适用于空间点。为了验证这一点,我们将两个数据集互换位置,做了对比实验,当用LineString或Polygon数据集构建Quadtree索引,用Point数据集查询时,计算耗时缩短1~2个数量级,如图5右边所示。从总体来看,KDtree索引适合为空间点构建索引,Quadtree和STRtree适合为线和面构建索引。Quadtree构建索引时间长,查询耗时短,STRtree构建索引时间短,查询耗时长,若以构建索引时间与查询计算时间之和作为评价指标,Quadtree性能优于STRtree。
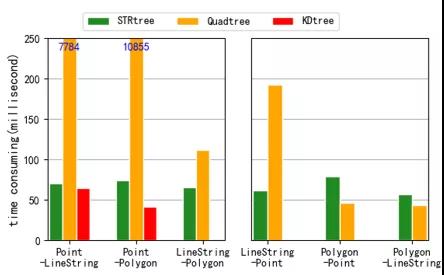
图5 空间拓扑连接性能 图6展示了空间距离连接运算(δ = 100米)的性能,在空间距离连接时,将 r . mbr 向外扩展 δ 的距离生成扩展最小边界矩形 r . embr (δ),用 r . embr ( δ )查询空间索引,然后判断空间对象 s 与 r 的距离 distance ( r , s )是否小于等于 δ 。图6中的实验结果变化趋势与图5中类似。需要注意的是,在空间距离连接中,Quadtree和STRtree的性能差异相较图5中变小了,说明STRtree在空间距离变化过程中性能更加稳定。另外,相同数据集之间的空间距离连接要比图5中的空间拓扑连接的耗时更短。主要原因是,虽然空间拓扑连接的结果要比空间距离连接的结果少,但是判断两个空间对象 r 和 s 的空间 intersects 关系(等价于 distance ( r , s ) = 0)要比判断 distance ( r , s ) ≤ δ 更耗时。
图6 空间距离连接性能 图7展示了kNN 连接运算的性能( k = 10),只有STRtree索引支持 kNN 查询。当Point数据集与其它数据集做 kNN 连接时,计算耗时较低且交换数据集时性能变化不大,因为点是最简单的空间对象,所以点与其它空间对象距离的计算复杂度最低。当LineString和Polygon做 kNN 连接时,其耗时相对较长且交换数据集时性能相差一倍,可以看出,为LineString构建STRtree索引比为Polygon构建索引性能更好, STRtree索引更适用于空间线。
图7 基于STRtree索引的空间k 最近邻连接性能
本文介绍了空间连接运算的定义和基于空间索引的空间连接运算方法。同时,本文介绍了3种常用的树结构的空间索引和各自的特点。最后,本文做了对比分析实验,以验证不同空间索引对不同空间对象的支持情况和性能差异,以便在不同的空间连接运算场景下,选择适当的空间索引,实现高效的查询和计算。 [1] Finkel RA, Bentley J L. Quad trees a data structure for retrieval on composite keys[J].Acta informatica, 1974, 4(1): 1-9. [2] R.Agrawal, C. Faloutsos, and A. Swami. 1993. Efficient similarity search insequence databases. Springer, 69-84. [3] Guttman,A., 1984. R-trees: a dynamic index structure for spatial searching (Vol. 14,No. 2, pp. 47-57). ACM. [4] S. T.Leutenegger, M. Lopez, J. Edgington, et al. STR: A simple and efficientalgorithm for R-tree packing. In ICDE, 1997. [5] https://github.com/locationtech/jts
发表评论
向 进行回复
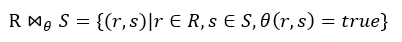 (1)
(1)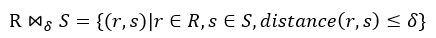 (2)
(2) (3)
(3)



0 条评论