02
12/2020

JUST技术：分布式时序相似查询初探

分类： 时空数据 | 浏览 (2078) | 评论 (0)
时序数据，即随时间变化的数据，在人们的日常生活中无处不在。过去的近十年来，随着电子监控和智能穿戴等设备的普及，更是产生了海量的时序数据。例如，经过多年的发展，火力发电行业的数字化程度已经达到了很高的水平，以一台60万千瓦的中型火电机组为例，其内置的上万个传感器，每秒可产生数万条实时监控数据。

其中，时序相似查询，即查询出与给定序列q最相似的k个序列，可用于推荐、聚类和异常检测等上层应用。在小规模数据下，时序相似查询是没有问题的，只要将给定序列q与数据库中所有数据进行两两相似性计算后取Top-k即可。
但是，在大数据的背景下，这种方法往往是行不通的，主要挑战体现在两个方面：第一，时序数据基数大，两两计算相似性哪怕是一种线性的解决方案（即仅需扫描一遍数据库），其耗时也是难以接受的；第二，时序数据维度高，两条时序数据计算相似性的耗时也随之增加。
针对挑战一，一种很自然的想法便是将相似的数据放在同一分区，查询时仅需扫描给定序列q所属的分区数据即可，无需全量扫描，这就是基于分布式存储数据的思想。针对挑战二，既然数据的维度高计算耗时，那么进行降维便可使计算成本下降，但如何在降维的同时又保持其在高维的相似性呢？
综上，本次技术分享，针对时序相似查询在大数据背景下遇到的困难，介绍几种基于分布式索引和查询的解决方案。

一、问题定义
下面给出一些基本定义。一条长度为n的时序数据X=<x1,x2,…,xn>，其中xi代表在某个时刻的读数，为了简单起见，我们假设每个读数的时间间隔相等，且xi为二进制0或1。数据库中存有海量的时序数据集合D={X1,X2,…}，相似查询指的是对于给定的查询序列q，返回与其最相似的k个时序数据。序列之间的相似性使用Jaccard相似度来衡量。设A和B是两个时序序列，其非零值个数分别为a和b，共有的非零值个数为c，则Jaccard相似度定义为： 
Jaccard相似度可以简单理解为A和B的交集与其并集的比值，当A等于B时，其交集等于并集，Jaccard相似度最大，为1；当A和B所有位均不相等时，其交集为0，Jaccard相似度最小，为0。所以两序列越相似，其交集也就越多，Jaccard相似度也就越大。

二、基于分区的解决方案
为了将相似的时序数据分至同一个分区，我们需要指定一些分区策略。
第一种想法自然便是划网格，我们想象一个维度为n（即时序数据的特征维度）的超立方体，将数据映射至该立方体，然后均匀地二分网格，显然，相近的序列很大可能会被划分至同一分区（少部分相似数据可能在分区边界附近被分隔开）。但是这样必然会导致数据的热点问题，即有的分区数据密集，有的分区数据稀疏甚至没有数据，这是因为划分网格时并没有考虑数据分布，如图1所示：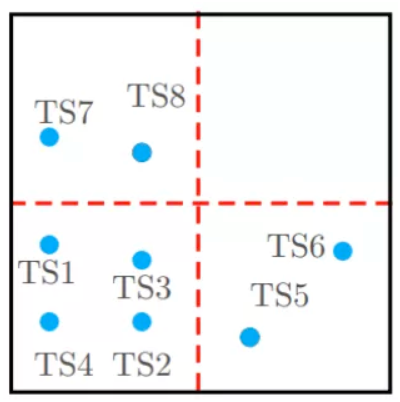 

图1 均匀二分网格（其中点表示二维的时序数据）
进一步，我们可以优化下划分网格的方法，不再一味地均匀划分，而是实时根据数据分布进行划分，总的原则就是尽量使网格中包含的数据量大致相等，例如基于KD树的思想划分网格并建立相应索引[2]，如图2所示：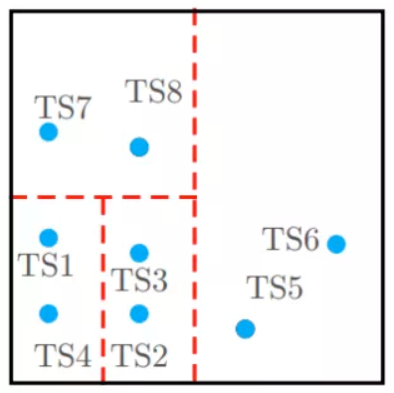 

 

图2 基于KD树的思想划分网格（保证每个网格中的数据量大致相等）
网格划分完成后，对于一个查询q，我们可以先计算其属于哪个分区，再将查询任务指派给该分区进行相似查询，这样便避免了数据的全量扫描。但是这样的查询存在一些问题，因为我们无法保证与q最相似的k条数据一定在同一分区，所以这只是一个近似的相似查询。当需要精确的相似查询时，不可避免的就需要扫描其它分区，但结合一些分区过滤规则，也可以大大减少数据的扫描量[2]。
 
三、基于降维的解决方案
对数据进行降维本身并不难，但在降维的同时保持数据高维时的相似性，却并不简单。这里简单其中的一种代表性算法：最小哈希算法（MinHash）。
设A和B分别为两个长度为n的时序序列，其值为二进制，<i1,i2,…,in>为其索引下标序列，其中ik在0至n之间。
MinHash的操作步骤如下：首先对<i1,i2,…,in>作一个随机打乱，并让A和B按打乱后的索引序列进行重新排列，然后分别取第一个非零行的索引下标作为其MinHash。这样得到的A和B的MinHash有一个重要的性质：

这里省去该性质的证明。这个性质为我们降维的同时保持相似性提供了可能。我们可以将上述步骤重复m次（m通常远远小于原序列的长度n），记录每一次的MinHash值得到序列<h1,h2,…,hm>，即得到两向量的Signature签名向量sig(A)=[h1(A),h2(A),…,hm(B)]和sig(B)=[h1(B),h2(B),…,hm(B)]。
这样我们既进行了降维（维度由n降维m，m远小于n），又近似保持了向量的相似性（sig(A)和sig(B)以概率保持A和B的Jaccard相似性），计算相似性时仅需计算Signature向量的相似性即可，降低了计算成本。

四、结合分区和降维的解决方案
上述的MinHash算法虽然将数据映射到低维空间中的签名向量，并近似保持了高维时数据之间的相似性，解决了挑战二中时序数据维度高的问题，但是仍需两两计算数据之间的相似性，没有解决挑战一。试想，若我们对降维后的数据再进行分区，是否可以得到更好的效果，具体思想是：先对原数据进行降维，再将降维后的数据分桶，将可能相似的数据以较大概率分至同一个桶内，这个每个时序数据的“备选相似数据集”就会相对较小，从而降低了寻找其相似数据的计算复杂度。其中，局部敏感哈希（Locality Sensitive Hashing，LSH）便是这类算法的代表。
LSH是建立在MinHash所得到的Signature向量基础上，将每一个向量等分为几段，称之为band，其基本思想是：若两个向量的一个或多个band相同，那么这两个向量的相似度高的可能性就较大。LSH的做法是，对每条数据的Signature向量在每一个band上分别进行哈希分桶（哈希算法并无特殊要求），任意一个band上被分到同一桶的数据就互为Candidate数据，这样仅需要计算Candidate数据集的相似性就可以找到每个数据的相似数据了。这里的分桶即为分区，利用分布式将数据存储在不同的分区上。
当然，LSH是一种基于概率的方法，必然会有漏网之鱼，所以我们希望以下两种情况的数据越少越好：1）False Positives：相似度低的数据被哈希到了同一个桶；2）False Negatives：相似度高的数据在每一个band上都没有被哈希到同一个桶。
当对序列q进行相似查询时，我们可以先计算q所属的桶编号，将查询下发至桶，最后进行整合取Top-k，这样大大过滤掉了不必要的相似性计算，同时也以概率保证了查询结果的正确性。但是，因为LSH是基于概率的，所以是一种近似的相似查询，并且不能处理精确的相似查询的需求。

目前，我们JUST正在构建自己的分布式时序数据平台，敬请关注。


参考文献：
[1] Alghamdi N, Zhang L, Zhang H, et al. ChainLink: Indexing Big Time Series Data For Long Subsequence Matching[C]//2020 IEEE 36th International Conference on Data Engineering (ICDE). IEEE, 2020: 529-540.
[2] Yagoubi D E, Akbarinia R, Masseglia F, et al. Massively distributed time series indexing and querying[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 32(1): 108-120.
[3] Gionis A, Indyk P, Motwani R. Similarity search in high dimensions via hashing[C]//Vldb. 1999, 99(6): 518-529.

« JUST技术：基于深度学习Seq2Seq框架的技术总结
JUST技术：当我停留时我在干什么? »

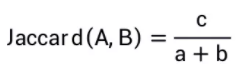
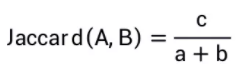
0 条评论

    正在加载评论...

    发表评论

    电子邮件地址不会被公开。 必填项已用 * 标注