2020年初,一场突如其来的新冠疫情,使得公共卫生安全问题受到了全社会的广泛关注。与此同时,如何及时掌握人与人之间的病毒传播路径,及时发现确诊人员的密切接触者,成为了各地政府疫情防控最迫切的需求。JUST基于大规模轨迹数据,针对易感人群难以发现的问题,开发并提供了关联人群查询功能,通过对轨迹进行匹配挖掘,能够快速找出与确诊人员行动轨迹在时空维度有过“接触”的人群。其中,实现该功能的很重要的一项工作就是:如何衡量两条轨迹的相似性。下文将简要介绍一些常见的轨迹相似性度量方法。轨迹作为一种时空数据[1],指的是某物体在空间中的移动路径,通常表示为GPS点的序列,例如tr=<p1→p2→…pn>,其中点pi=(lat,lng,t),表示该物体在t时刻位于地理坐标位置(lat,lng)上,lat和lng分别表示纬度和经度。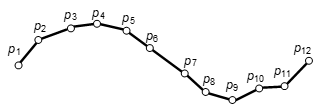
大数据时代,随着车载导航系统的普及,海量的轨迹数据正在源源不断的产生,这些轨迹中蕴含着巨大的价值[2],例如可以进行交通流量分析和预测,为政府的城市规划提供建议;也可以进行轨迹聚类,发现那些被很多轨迹经过的道路,用于指导自行车道的规划;还可以进行驻留点检测,发现轨迹经常停留的区域等。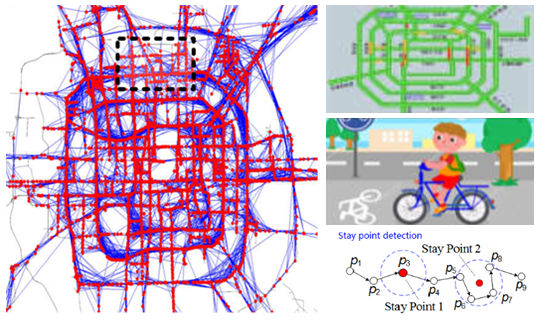
轨迹数据的分析处理非常具有挑战性,主要包含三个方面:1)轨迹数据量大;2)轨迹数据噪音多;3)轨迹数据获取途径多样。其中,轨迹相似性作为一项基础算法服务,衡量两条轨迹之间的距离大小,可为其上层应用提供支持,也是目前研究的热点之一。
相对于点与点或点与轨迹之间的距离度量,轨迹之间的距离度量更加的复杂,需要考虑的因素也更多,例如轨迹的采样率、考虑轨迹的时间信息和轨迹自身的噪音等。常见的轨迹相似性度量方法大致分类如下图所示。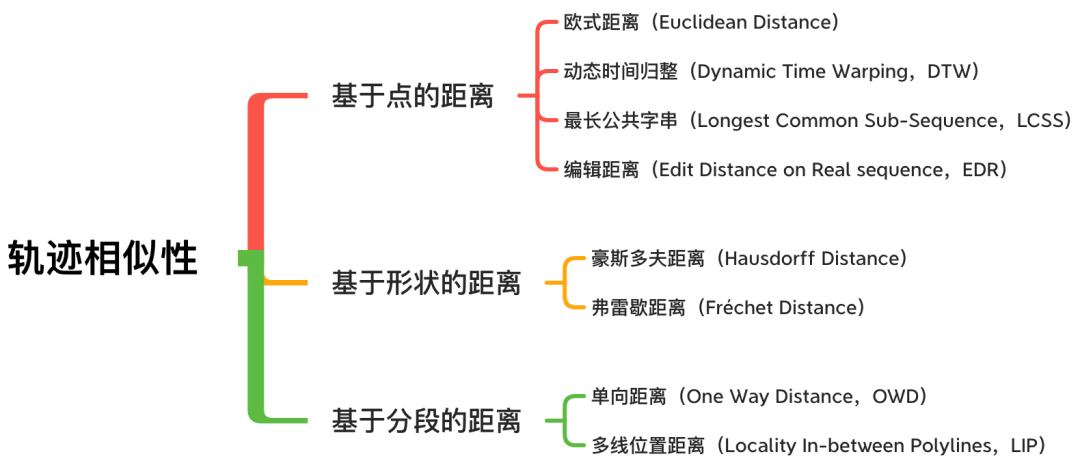
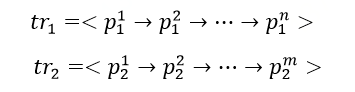
欧式距离要求两条轨迹的长度相同一一对应,其数学定义为: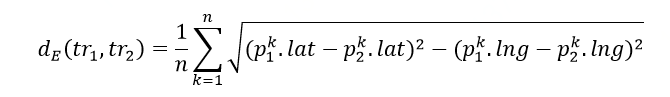
欧氏距离的定义简单明了,就是两条轨迹对应点的空间距离的平均值,但是缺点也很明显,就是不能度量不同长度的轨迹相似性,且对噪音点敏感。
- 动态时间归整(Dynamic Time Warping,DTW)
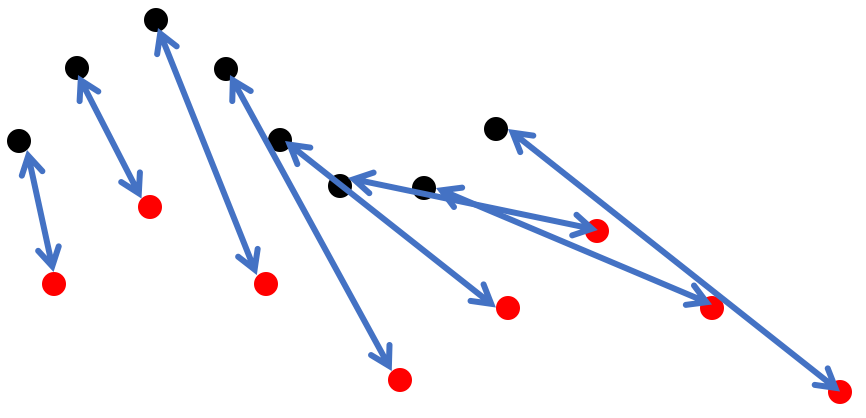
如上所述,欧式距离的一个明显的限制是要求两条轨迹长度相等,这在实际情况中是不太可能的,更理想的情况应该在轨迹长度上具有一定的灵活性。动态时间归整DTW[3]的思想是自动扭曲两个序列,并在时间轴上进行局部的缩放对齐,以使其形态尽可能一致,从而得到最大可能的相似性。DTW将两条轨迹的点进行多对多的映射,从而较为高效地解决了数据不齐的问题,其动态规划算法如下: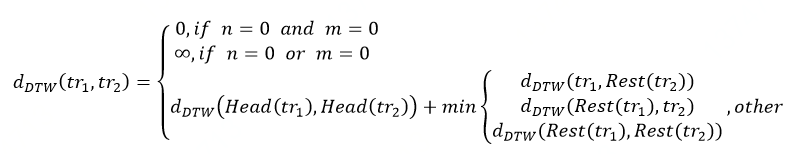
其中Head(tr)=<p1>表示该轨迹的第一个点;Rest(tr)=<p2…pn>表示除第一个点之外的所有点组成的子序列。
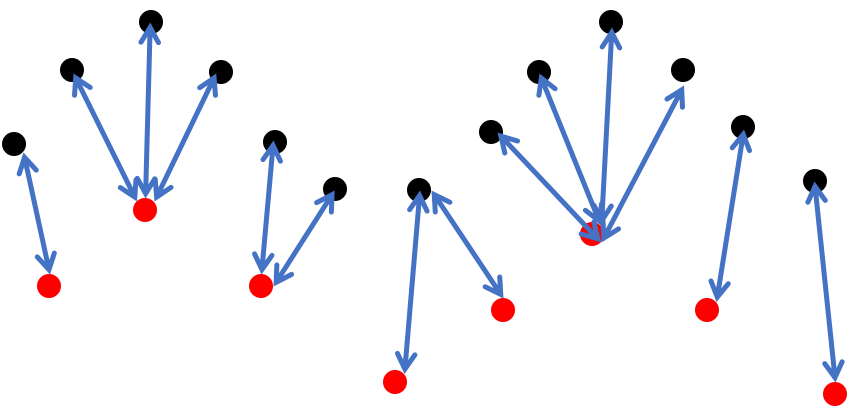
动态时间归整算法灵活,对轨迹长度无限制,且效果较好,但是其并未对噪音点进行处理,离群点也会对结果造成较大影响。- 最长公共字串(Longest Common Sub-Sequence,LCSS)
有一个经典的算法问题:求解两序列的最长公共子序列,不要求公共子序列中的两个连续相连,例如BDCABA和ABCBDAB的最大公共子序列为BCBA。在此基础上,很自然提出了基于最长公共子序列的轨迹相似性度量方法,即LCSS,其值代表最多可被是为同一点的点数,也就是两条轨迹中满足最小距离阈值限制的轨迹点的对数。其基于动态规划的算法如下: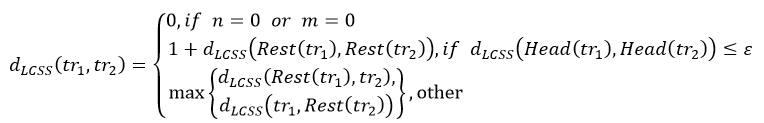
其中,参数是最小距离阈值,两点之间距离小于该值时将被认为是同一点,此外,该算法对轨迹长度没有限制。
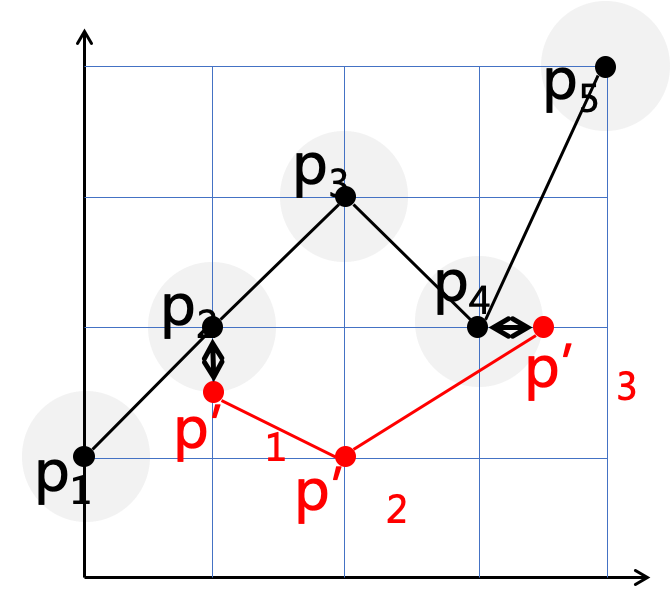
图7:LCSS示意图,有两对点的距离小于,则被视为同一点,LCSS值为2最长公共子串距离对噪音点进行了处理,即因噪音点的偏离没有与其相近的轨迹点故不会被计算在最终结果内,这一步骤有效对抗噪音。但与此同时,该算法的最小距离阈值不好定义,还有可能返回并不相似的轨迹。- 编辑距离(Edit Distance on Real sequence,EDR)
给定两个长度分别为n和m的轨迹tr1和tr2,最小距离的匹配阈值,则两条轨迹之间的EDR距离[4]就是需要对tr1及逆行插入、删除或替换使其变为tr2的操作次数,其基于动态规划的算法如下。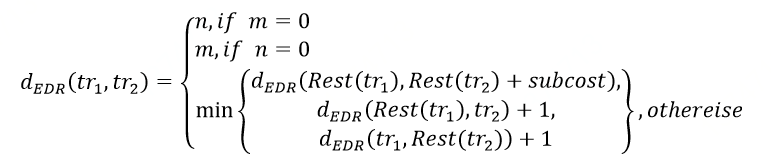
其中,
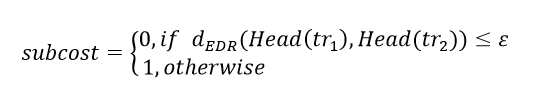
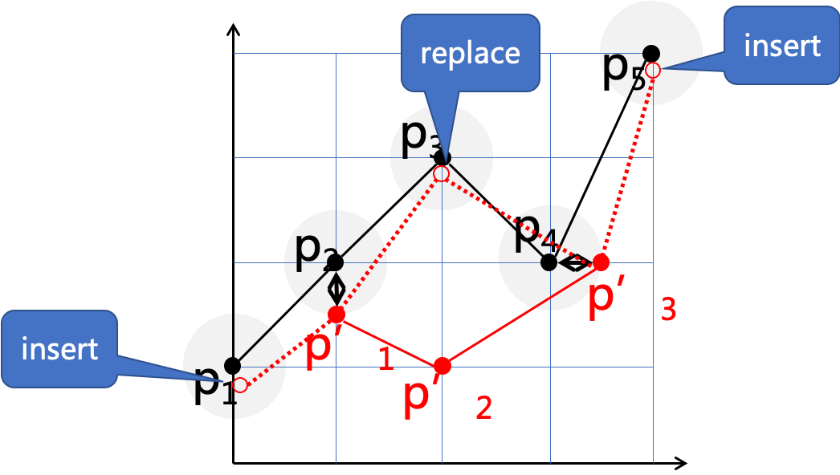
图8:EDR示意图,在p1处“插入”一点、将p2'“替换”为p3和在p5处“插入”一点,共计3个操作使两条轨迹相等(即对应点距离均小于阈值),故其EDR值为3轨迹的编辑距离为轨迹相似新度量提供了一种新的思路,其缺陷也很明显,就是对噪音点敏感。- 豪斯多夫距离(Hausdorff Distance)
简单来说,豪斯多夫距离[5]就是两条轨迹最近点距离的最大值。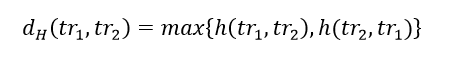
其中,h(tr1,tr2)称为tr1到tr2的单向豪斯多夫距离,其定义如下:
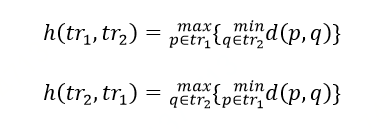
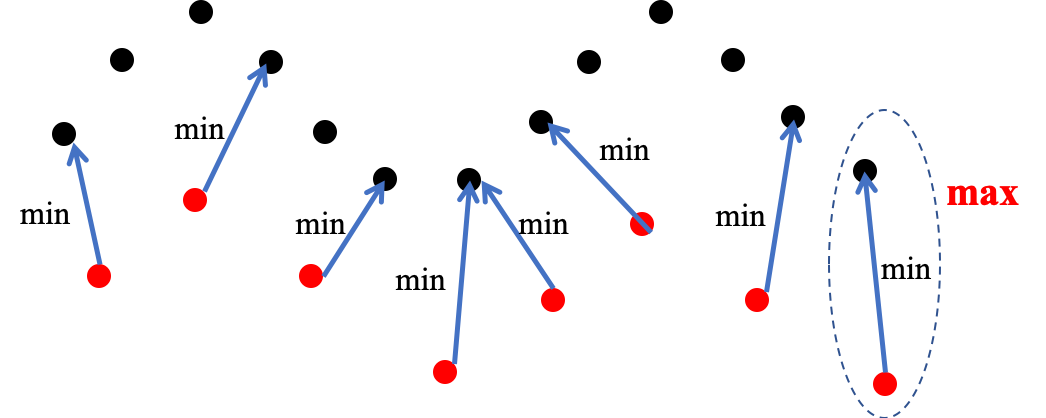
图9:豪斯多夫距离示意图,每个红点都有一个最近的黑点,豪斯多夫距离就是其中的最大值直观的理解,弗雷歇距离[6]就是狗绳距离,即主人走路径A,狗走路径B,各自走完两条路径过程中所需要的最短狗绳长度。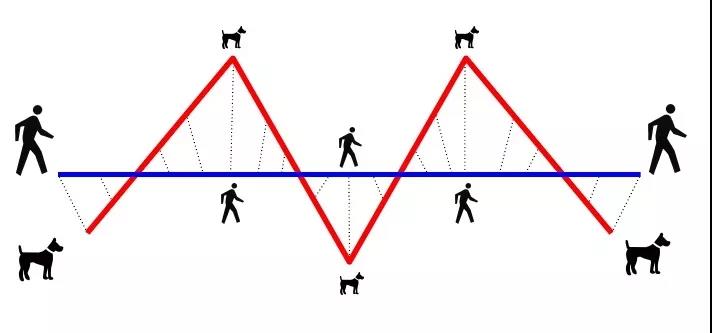
图10:狗绳距离示意图,虚线表示主人和狗在同一时刻所处位置的对应,弗雷歇距离即为长度最长的虚线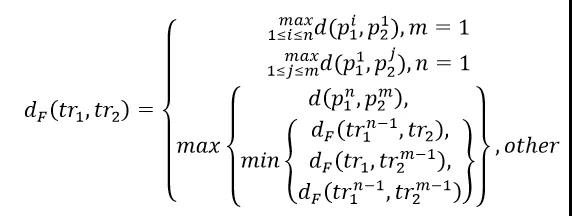
其中,d(p,q)是两个GPS点的欧式距离,tr(n-1)=<p1→p2→…pn-1> 是轨迹tr的长度为n-1的子轨迹。弗雷歇距离为我们提供了一种简单直观的度量相似性的方式,也能达到较好的效果;但可惜的是其并没有对噪音点进行处理,例如若狗的某个轨迹点因为噪声偏离得很远,那么弗雷歇距离也随之增大,这显然是不合理的。- 单向距离(One Way Distance,OWD)
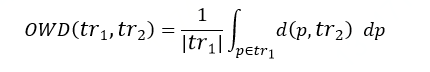
其中,|tr1|表示轨迹tr1的长度,d(p,tr2)表示GPS点p到tr2的距离。为了对称,简单修改上述公式:
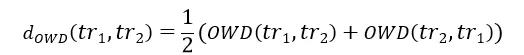
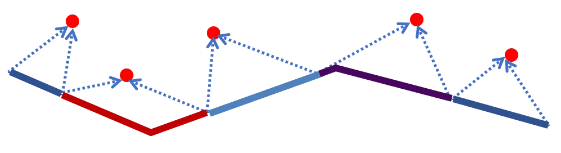
图11:单向距离示意图,该距离即为各多边形的面积之和与折线长度的比值OWD距离的基本思想基于两条轨迹围成的面积,当面积大,说明轨迹之间距离较远,相似度就低;相反,若围成的面积为0,则说明两条轨迹重合,相似度最高。- 多线位置距离(Locality In-between Polylines,LIP)
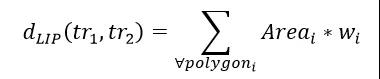
其中,Ii表示两条轨迹的第i个交点,权重wi定义如下:
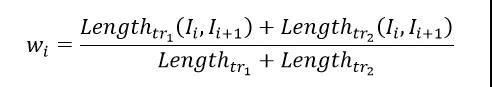
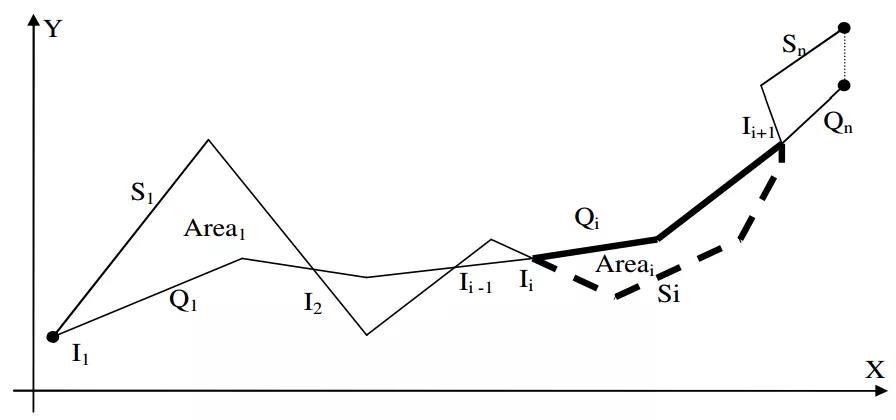
图12:LIP方法示意图,该距离为每个区域面积与其权重乘积之和LIP方法很好理解,当某区域面积的周长占总长比重大时权重也自然就大;当Area均为0时,说明两条轨迹重合没有缝隙,LIP距离为0;当Area加权和大时,则说明两条轨迹之间缝隙较大,LIP距离也就大。此外,权重由区域周长占总长比重大决定,也一定程度对抗了噪音点的干扰。目前,京东城市自研的时空数据引擎JUST(JD Urban Spatio-Temporal Data Engine)已经实现了动态时间规整、豪斯多夫距离和弗雷歇距离等多种轨迹相似性计算方法,用户无需编码,仅需一条SQL就可以实现,同时JUST还提供了轨迹的可视化功能方便用户观察,欢迎访问https://just.urban-computing.cn/进行体验,合作请发邮件至just@jd.com。
图13:JUST产品主页
[1] Zheng, Y., et al. Urban Computing: concepts, methodologies, and applications. ACM TIST.[2] Yu Zheng. Trajectory Data Mining: An Overview. ACM Transactions on Intelligent Systems and Technology. 2015, vol. 6, issue 3.[3] Yi B K, Jagadish H V, Faloutsos C. Efficient retrieval of similar time sequences under time warping[C]//Proceedings 14th International Conference on Data Engineering. IEEE, 1998: 201-208.[4] Chen L, Özsu M T, Oria V. Robust and fast similarity search for moving object trajectories[C]//Proceedings of the 2005 ACM SIGMOD international conference on Management of data. 2005: 491-502.[5] Alt H. The computational geometry of comparing shapes[M]//Efficient Algorithms. Springer, Berlin, Heidelberg, 2009: 235-248.[6] Eiter T, Mannila H. Computing discrete Fréchet distance[R]. Technical Report CD-TR 94/64, Christian Doppler Laboratory for Expert Systems, TU Vienna, Austria, 1994.[7] OWD论文:Lin B, Su J. One way distance: For shape based similarity search of moving object trajectories[J]. GeoInformatica, 2008, 12(2): 117-142.[8] LIP论文:Pelekis N, Kopanakis I, Marketos G, et al. Similarity search in trajectory databases[C]//14th International Symposium on Temporal Representation and Reasoning (TIME'07). IEEE, 2007: 129-140.




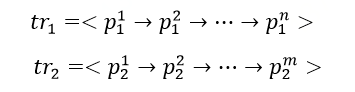
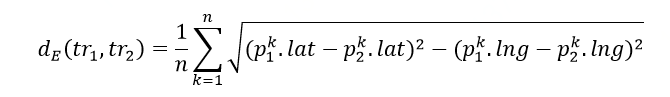

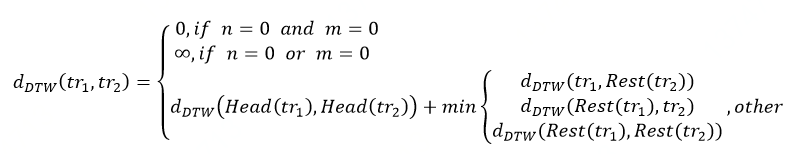

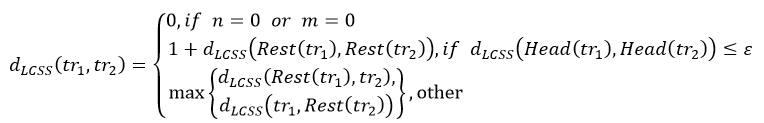

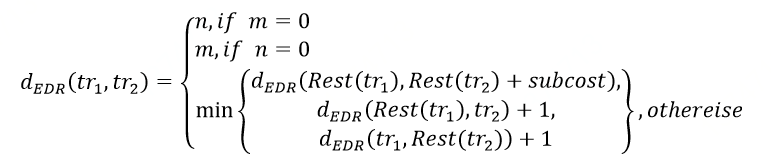
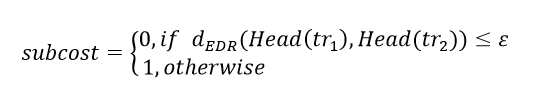

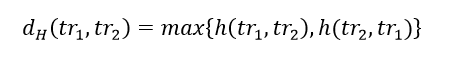
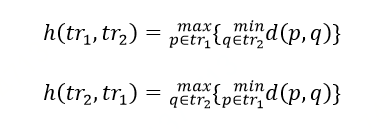


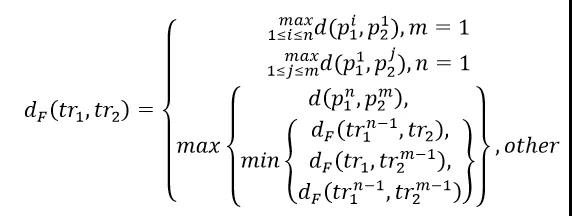
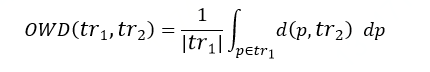
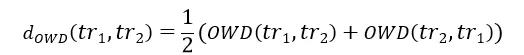

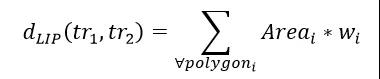
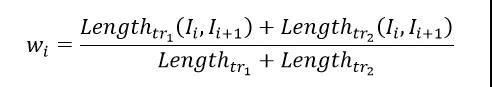




0 条评论