14
12/2020

JUST技术：从空间关系到空间连接，JUST提升信息挖掘意义

分类： 时空数据 | 浏览 (2833) | 评论 (0)

现实世界中存在大量的与空间相关的数据，如停车场位置、河流、轨迹等。这些空间数据之间存在很多空间关系，如相离、相交、包含等。在实际工作中，这些空间数据经常会使用空间连接操作把两个空间数据集通过空间关系连接起来。如根据两个数据集行政区域和poi，统计出每一个行政区中包含的poi类别为加油站的数量。

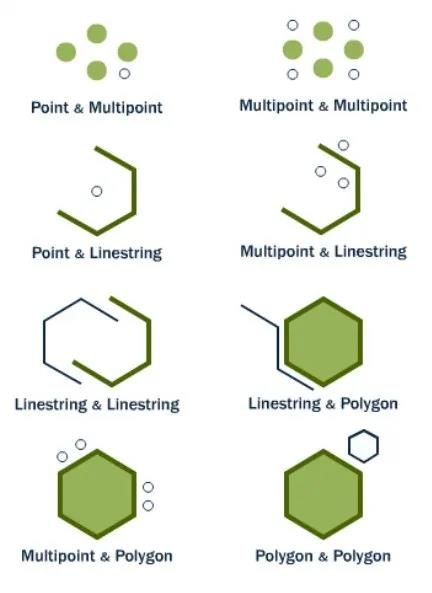
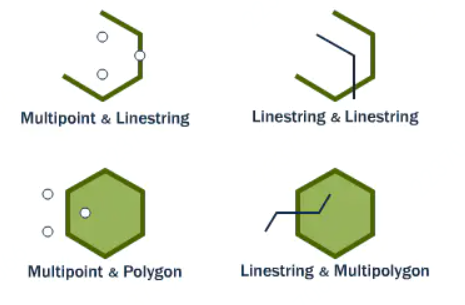
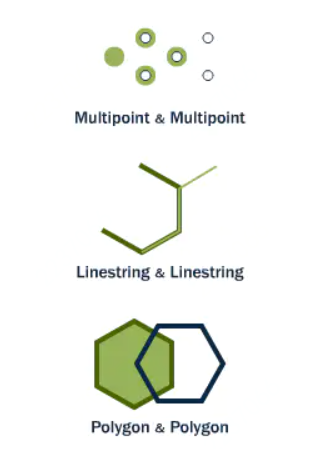
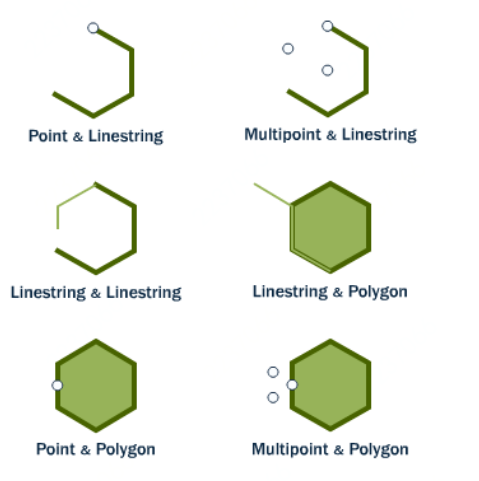
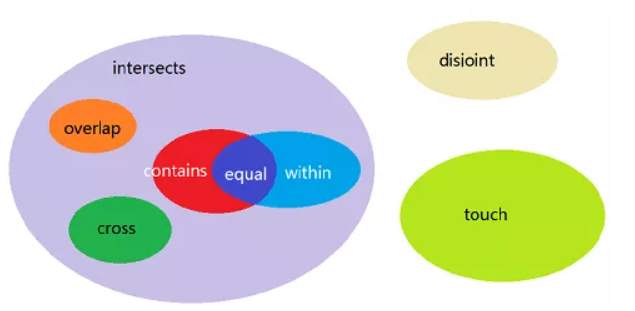
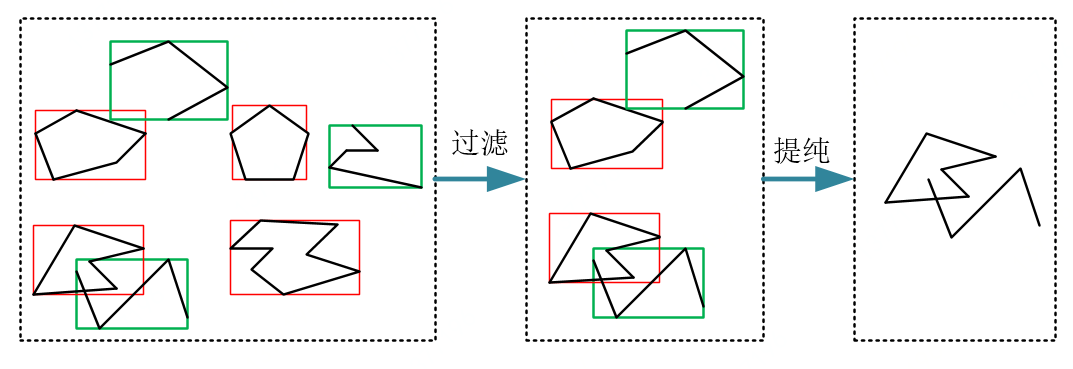
本次技术分享将空间数据中常用的空间关系和空间连接算法。首先将介绍空间数据的基本概念，再详细介绍OGC标准定义的比较两个几何图形关系的方法，并通过实例展示在空间关系基础上空间维度信息的统计和挖掘；其次将数据从两个几何图形扩展到两个空间数据集，介绍空间连接的定义和经典算法；最后简要描述JUST目前在空间连接方向上的研究。

一、背景介绍
空间数据，也被称作地理空间数据，是一种用点(point)、线(linestring)、面(polygon)等基本空间数据结构来表示人们赖以生存的自然世界的数据，现实世界中的数据有80%与地理位置有关，如公园、河流、道路、轨迹等。
常见的空间数据类型有以下3种：
以GPS点、交叉路口为代表的点数据；以路段为代表的线数据；以行政区域为代表的面数据，如图1。     
图1 JUST中渲染的点、线、面数据 
不同于普通数值数据大于、小于或等于的关系，空间数据作为几何图形会有不同的空间关系，比如我们可以通过判断两条轨迹是否相交去判定轨迹对象是否经过同一个地方，在本文的第二部分将会详细介绍空间数据之间的空间关系。
空间关系可以应用在很多场景中，如根据两个数据集行政区域和poi，统计出每一个行政区中poi类别为加油站的数目。为了加快两个数据集中空间数据的关系判断速度，很多空间数据库都提供了高效的空间连接操作。在本次分享的第三部分将会详细介绍空间数据库空间连接操作，并介绍一个传统的空间连接算法plane sweep。
在本文的最后，总结了空间关系判断对于空间信息挖掘的意义以及介绍了JUST目前实现空间连接操作的方法和未来的相关研究。   
 
二、空间关系(spatial relation)
空间关系是指各实体空间之间的关系，包括拓扑空间关系，顺序空间关系和度量空间关系，本文重点介绍拓扑空间关系。在空间数据库中通常会以ST_开头的空间谓词去判断两个空间对象是否满足某种关系，返回true或false。 
1.equal(相等)：用于测试两个图形的空间对等性。如果两个相同类型的几何图形具有相同的坐标信息，则两个图形是相等的，这种空间关系可以实现空间对象的精准查询。
2.disjoint(相离)：两个任意类型的几何形状没有相交的部分，直观的表示如下：
图2 disjoint关系的图形表示
3.intersects(相交)、crosses(相穿)、overlaps(重叠)：这三个空间关系都用于检测两个几何图形是否存在相交关系。其中intersects为广义的相交，包含了crosses和overlap两种关系，crosses和overlap对相交图形的维度有一定要求。
intersects用于测试两个几何图形是否有公共部分，是disjoint的相反表示。intersects使用范围广泛，比如判断两条轨迹是否经过同一个地方，需要判断两条轨迹的空间线是否相交；找出长江流经的所有省份的名称，需要判断河流(线)和行政区(面)是否相交。
当两个几何图形的相交部分的几何维度比这两个几何图形的最高维度低一个维度，则称两者满足cross关系。如图3，线和线的相交产生点满足cross关系，即两个维度为1的图形(线)相交产生维度为0的图形(点)。
图3 crosses关系的图形表示
当两个几何图形的维度相同时，它们相交产生的几何图形与原图形维度相同，则称两者满足overlap关系，如图4，面和面相交产生面满足overlap关系，即两个维度为2(面)的图形相交产生维度为2的图形(面)，且产生的图形与原图形不同。
图4 overlap的图形表示
4.touch(相连)：表示两个图形它们在边界上接触，但是内部并不相交，如图5。

图5 touch关系的图形表示
5.within、contains(包含)：contains和within都表示两个几何图形的包含关系，不过主语相反。within(A ,B)用于判断A是否在B的内部，contains(A, B)用于判断A中是否包含B。比如确定每一个行政区块内类型为加油站的poi，就需要判断加油站是否在该行政区块内部。
6.dwithin(距离包含)：实际场景中有一个比较常见的问题“寻找在京东集团总部1000m内的所有公交车站”。显然，单纯就空间对象而言公交车站和京东总部是一个相离的关系。但是，实际上它们也存在了一种距离相交关系，在空间数据库中可以使用st_Dwithin去判断两个空间数据的距离关系。
通过上述的介绍，可以发现空间关系之间，可能是完全互斥的，比如disjoint和intersects，contains和within。也有重叠的部分，比如intersects、crosses、overlap等。如图6，这幅图能够更直观地表示这些关系的“关系”。
图6 空间关系文氏图

三、空间连接（spatial join）
读到这里，想必你对空间关系有一定的了解了，回到“如何去统计在每一个行政区中poi类别为加油站的数目”这个问题。在空间数据库中，行政区和poi是两个数据集，除了空间关系两个数据集可能并不存在相同的属性字段，那么如何连接这两个数据集呢？显然我们需要利用两组空间数据对应的空间关系了。而这种使用空间关系作为连接键来连接来自不同数据表的操作被称为空间连接（spatial join）。
目前空间连接处理一般分为两个步骤，（1）过滤（filter）（2）提纯（refinement），如图7。在上述的例子中，我们可以计算出每一个行政区对应的MBR（能完全包含整个行政区的最小矩形），再与加油站的位置信息进行空间连接，得到对应区域空间范围的数据集，粗略地选出在对应区域的候选加油站；在对应区域的数据集内，再判断每一个候选连接中加油站与行政区的真实关系是否为包含关系，去除不符合关系的连接，从而得到较为准确的结果。

图7 空间连接的处理步骤


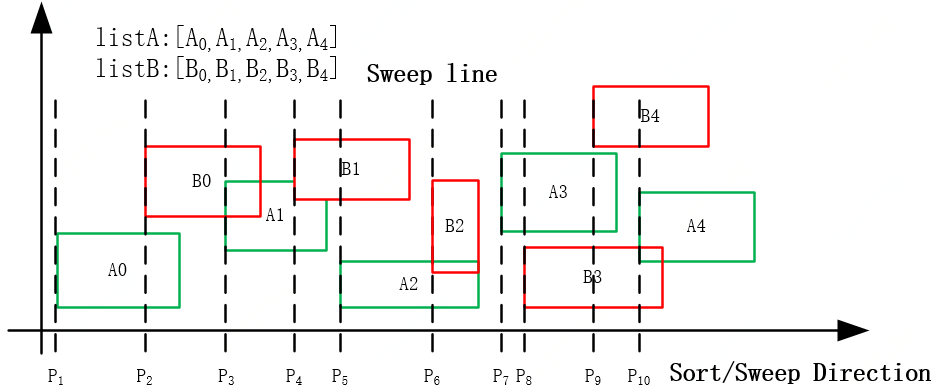
其中，过滤操作是第一步也是十分重要的一步，它可以缩小计算范围，避免大量无用计算。空间数据库实现过滤操作使用的最经典算法之一是plane sweep，这个算法通过一趟扫描，找出具有某种连接关系的几何对象对集合，避免了join的嵌套循环（nested loop join）。
Plane sweep算法主要分为两个步骤，以相交关系为例，假设几何对象都被抽象为MBR（最小矩形），如图8所示，Planesweep算法如下：
1.分别对两个集合A, B的矩形按照某一指标排序（比如，按照左边框从小到大）,如图8，形成ListA, ListB两个顺序集合；
2.从左向右扫描已排好序的集合，并标注一些检测点（如图p1, p2等），按照算法定义追踪active矩形（与当前检测点垂线相交的矩形），并判断active矩形集合间的相交关系，得到结果。
图8 Plane sweep 算法图解
算法流程：
图9 Planesweep 算法流程 
那么如何去追踪active矩形呢？plane-sweep算法定义了一个支持三种数据操作的数据结构sweepStruture，操作分别是insert、remove-inactive、search。这三种操作可以即时追踪与当前检测点所在扫描线(sweep line)相交的矩形，移除不重叠的矩形，不断缩小搜索的范围。比如对于图一中的检测点p1，扫描线与ListA中的A0相交，sweepStructure(A)实现insert(A0)，sweepStructure(B)为空，ListA的第一个元素指向A1；对于检测点p3, 扫描线与A1相交，且在这次扫描中A集合的开始位置先于B，所以sweepStructure(A)实现insert(A1)，删除不与给定重叠的矩形，再搜索sweepStructure(A)和sweepStructure(B)中满足相交关系的几何对，本次搜索输出{A1, B0}。
Plane-sweep算法的时间复杂度为O(nlog(n))。假设数据集的规模为n (表示两个数据集的规模之和)，plane-sweep搜索操作的时间复杂度为O(log(n))，而最多会进行n次搜索，因此总的时间复杂度O(n^2)降低到了O(nlog(n)）。
除了平面扫描算法，很多空间数据库还利用了空间索引实现了大数据集的空间连接。常用于空间连接操作的空间索引有R-tree，KD-tree等。JUST提供了一套高效的时空索引（Z2、XZ2等）[4]，大大地降低了空间连接时所需要的比较次数，提高了效率。

四、小结 
空间关系的判断可以帮助我们实现很多空间维度信息的统计和挖掘，比如统计行政区中路网长度的总和，统计某一地块的poi分布、人口密度等，对于道路建设、兴趣地点推荐等都有很大帮助，本文介绍了空间关系和经典的空间连接算法。
目前JUST已经兼容主流空间数据库的空间关系函数，实现两个空间对象的空间关系判断。此外，为了高效支持海量时空数据的空间关系判断、连接，并实现更多的关联筛选功能，JUST正在研发基于NoSQL的高效空间连接，对海量时空数据进行分区索引，整体架构将融合关系连接、距离连接和KNN连接, 敬请期待！
 
参考文献
[1]EDWIN H. JACOXand HANAN SAMET: Spatial Join Techniques[J] // ACM Transactions on Database Systems, Vol. V, No. N, November 2006.
[2] https://en.wikipedia.org/wiki/DE-9IM
[3] PostGIS 3.0.4dev Manual
[4] Li, Ruiyuan, et al. "Just: Jdurbanspatio-temporal data engine." 2020 IEEE 36thInternationalConference on Data Engineering (ICDE). IEEE, 2020.

« JUST技术：当我停留时我在干什么?
JUST技术：基于无参生成模型的轨迹生成 »

0 条评论

    正在加载评论...

    发表评论

    电子邮件地址不会被公开。 必填项已用 * 标注