康瑞部落

1. 课程题目

给定不受限优化问题：

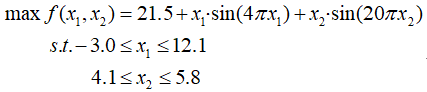
实现遗传算法，得出结果，并画出寻优曲线。

2. 算法总框架

算法框架的代码如下：

int generation = 0;
List<Chromosome> current = Initial();
Fitness(current);

while(generation < _maxGeneration)
{
	var crossChildren = Crossover(current);
	var mutationChildren = Mutation(current);
	current.AddRange(crossChildren);
	current.AddRange(mutationChildren);
	Fitness(current);
	current = Selection(current);
	generation++;
}

算法整体分成两步：

（1） 初始化（算法第2行）。随机初始化生物种群，current表示当前生物种群，然后计算当前生物种群的适应度。

（2） 进化（算法第5-14行）。算法进化指定迭代最大次数_maxGeneration，每次迭代执行4个操作：

        a)  交叉遗传（算法第7行），得到一些子代crossChildren。

        b)  变异遗传（算法第8行），得到一些子代mutationChildren。

        c)  计算所有子代和父代的适应度（算法第11行）。

        d)  从所有子代和父代中选择一些个体形成当前种群（算法第12行）。

下面的小节对每个操作进行详细介绍。

3. 初始化Initial

该操作随机产生_popSize个个体形成种群，并返回。其代码如下所示：

protected List<Chromosome> Initial()
{
	List<Chromosome> result = new List<Chromosome>();
	for(int i = 0; i<_popSize; i++)
	{
		double num1 = RandomNumber(MIN_X1, MAX_X2);
		double num2 = RandomNumber(MIN_X2, MAX_X2);

		result.Add(Encode(num1, num2));
	}
	return result;
}

针对每个产生的个体，我们产生两个给定范围的随机数，然后对这两个随机数进行编码，得到该个体的染色体。Encode方法的代码如下：

private Chromosome Encode(double num1, double num2)
{
	num1 = (num1 - MIN_X1) * (Math.Pow(2, _code1Len) - 1) / (MAX_X1 - MIN_X1);
	num2 = (num2 - MIN_X2) * (Math.Pow(2, _code2Len) - 1) / (MAX_X2 - MIN_X2);

	var str1 = DecToBinary((int)num1);
	var str2 = DecToBinary((int)num2);
	
	while(str1.Length < _code1Len)
	{
		str1 = '0' + str1;
	}

	while(str2.Length < _code2Len)
	{
		str2 = '0' + str2;
	}

	var str = str1 + str2;

	Chromosome c = new Chromosome(str);

	return c;
}

这里第3行和第4行的_code1Len和_code2Len分别表示用二进制字符串表示x1和x2的给定范围所需要最少位数。程序第3行和第4行将原始数字均匀映射到0到2len-1中的某个数字，然后将所得结果转化成二进制表示的形式。第9至17行是对齐操作，将不足长度的二进制串前面补0。最后得到整个二进制字符串，生成单个个体。变量所需的二进制位数len的计算公式为：

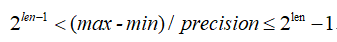
其中max和min分别表示变量的最大和最小的范围，precision表示的精度，若小数点保留5位小数，则precision = 10-5。

4. 适应度计算Fitness

这一步计算给定一代种群的最优值，并保存历史最佳结果。其代码为：

protected void Fitness(List<Chromosome> chs)
{
	double temMaxValue = double.MinValue;
	double optimalX1 = 0;
	double optimalX2 = 0;
	foreach(var ch in chs)
	{
		var decode = Decode(ch);
		var value = ValueFunction(decode.Item1, decode.Item2);
		if(value > temMaxValue)
		{
			temMaxValue = value;
			optimalX1 = decode.Item1;
			optimalX2 = decode.Item2;
		}
	}
	_localMaxValue.Add(temMaxValue);
	if(temMaxValue > _maxValue)
	{
		_maxValue = temMaxValue;
		_optX1 = optimalX1;
		_optX2 = optimalX2;
	}
	_globalMaxValue.Add(_maxValue);
}

算法中第6至17行找到当前一代的最优值，第18至24行替换全局最优值。对于某个个体而言，计算它的适应度分成两步：解码（第8行）和值计算（第9行）。

(1)首先对其染色体进行解码，代码如下所示。染色体是一个固定长度的二进制字符串，首先取出每个变量对应的部分（第3和4行），然后将二进制字符串转化成十进制数，注意这个十进制数是0至2len-1对应的数字，我们还需要转化成实际区间内的数（第9和10行）。

private Tuple<double, double> Decode(Chromosome ch)
{
	Chromosome ch1 = ch.SubChromosome(0, _code1Len - 1);
	Chromosome ch2 = ch.SubChromosome(_code1Len, _code1Len + _code2Len - 1);

	double num1 = BinaryToDec(ch1.ToString());
	double num2 = BinaryToDec(ch2.ToString());

	num1 = MIN_X1 + num1 * (MAX_X1 - MIN_X1) / (Math.Pow(2, _code1Len) - 1);
	num2 = MIN_X2 + num2 * (MAX_X2 - MIN_X2) / (Math.Pow(2, _code2Len) - 1);

	return Tuple.Create<double, double>(num1, num2);
}

(2)值计算是指将得到的变量代入到原方程函数中求得所得的值。

5. 交叉遗传Crossover

交叉遗传是指交换两个个体的部分DNA，形成新的个体。如下图所示，两个个体v1和v2在第17个位置之后的部分交换后，得到新的个体c1和c2。

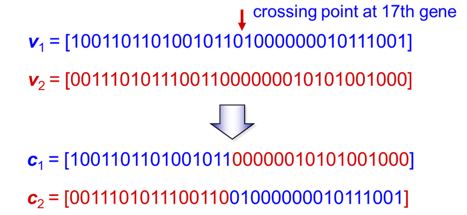
交叉遗传的代码如下图所示。该算法给定一定数目的父种群，产生相同数目的子种群。_pCrossover表示两个个体发生DNA交换的概率。

protected List<Chromosome> Crossover(List<Chromosome> chs)
{
	List<Chromosome> result = new List<Chromosome>();
	for(int k = 0; k < chs.Count / 2; k++)
	{
		if(_pCrossover >= RandomNumber(0, 1))
		{
			int i = 0, j = 0;
			while(i == j)
			{
				i = (int)RandomNumber(0, chs.Count - 1);
				j = (int)RandomNumber(0, chs.Count - 1);
			}
			int p = (int)RandomNumber(1, _code1Len + _code2Len - 2);
			var ch1 = new Chromosome(chs[i].SubChromosome(0, p - 1).ToString() 
						+ chs[j].SubChromosome(p, _code1Len + _code2Len - 1).ToString());
			var ch2 = new Chromosome(chs[j].SubChromosome(0, p - 1).ToString() 
						+ chs[i].SubChromosome(p, _code1Len + _code2Len - 1).ToString());
			result.Add(ch1);
			result.Add(ch2);
		}
	}
	return result;
}

6. 突变Mutation

突变是指更改部分DNA，生成新的个体。下面给出了突变的代码，对于每个个体的每个位置的DNA，随机进行翻转，然后形成新的个体。

protected List<Chromosome> Mutation(List<Chromosome> chs)
{
	List<Chromosome> result = new List<Chromosome>();
	foreach(var ch in chs)
	{
		BitArray genes = new BitArray(ch.Genes);
		for(int j = 0; j < _code1Len + _code2Len; j++)
		{
			if(_pMutation >= RandomNumber(0, 1))
			{
				genes.Set(j, !genes.Get(j));
			}
		}
		result.Add(new Chromosome(genes));
	}
	return result;
}

7. 选择Selection

选择操作从一个群体中，选择一定数目的个体。个体被选择的概率正比于个体适应环境的程度。也就是说，若个体更适应环境，则被选择的概率越大。这相当于乐透游戏（Roulette Game），如下图所示，在一个转盘中有很多区域，每个区域的面积表示适应程度，随机旋转这个转盘，面积越大的区域指向某个区域的概率越大。

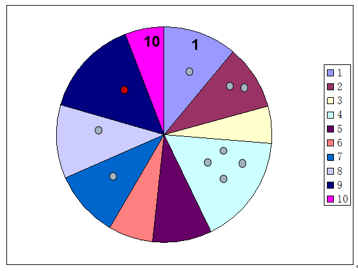
选择步骤的代码如下所示。代码第4至9行计算每个个体的适应度；第11至16行计算每个个体的适应度占总适应度的比例；第18至23行计算累计概率密度；第25至37行选择指定数目的个体。

protected List<Chromosome> Selection(List<Chromosome> chs)
{
	List<Chromosome> result = new List<Chromosome>();
	List<double> values = new List<double>();
	foreach(var ch in chs)
	{
		var decode = Decode(ch);
		values.Add(ValueFunction(decode.Item1, decode.Item2));
	}

	double F = values.Sum();
	List<double> ps = new List<double>();
	foreach(var value in values)
	{
		ps.Add(value / F);
	}

	List<double> cdf = new List<double>();
	cdf.Add(0);         //在开始填上0，方便后面编程
	for(int i = 0; i < ps.Count; i++)
	{
		cdf.Add(ps[i] + cdf[i]);
	}

	for(int i = 0; i < _popSize; i++)
	{
		double r = RandomNumber(0, 1);
		int j = 0;
		for(j = 0; j < cdf.Count - 1; j++)
		{
			if(r >= cdf[j] && r < cdf[j + 1])
			{
				break;
			}
		}
		result.Add(chs[j]);
	}
	return result;
}

8. 代码实现与结果

8.1 实验代码

实验采用C#语言，共有3个代码文件

(1)    Program.cs是程序入口。

(2)    GeneticAlgorithmSimple是整个遗传算法的实现类。

(3)    Chromosome是个体类。

8.2 实验参数

交叉遗传的概率_pCrossover = 0.25

突变的概率_pMutation = 0.01

一代种群中个体的数目_popSize = 10

最大迭代次数_maxGeneration = 1000

结果的精度PRECISION = 0.0001

8.3 实验结果

结果的进化过程如下所示，其中Local表示单代最优适应度随着代数的变化，Global表示全局适应度随着代数的变化。

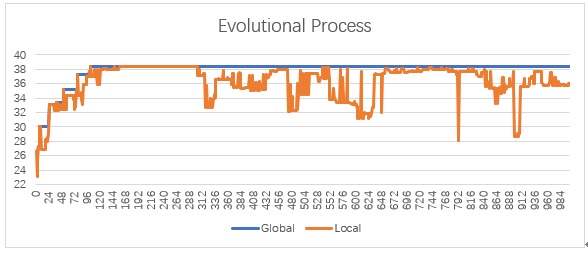
大约在第100代时，就已经达到了全局最优，此时：

X1 = 11.6281808020813

X2 = 5.72503128147221

F(X1, X2) = 38.8439131372254

所有源代码在Github中可以获得：https://github.com/IrisLoveLeo/GeneticAlgorithmSimple