康瑞部落

Douglas-Peucker algorithm is an error bounded sequence simplication. It is used for compressing trajectory, roadnetwork, etc. It's main idea can be shown as the following picture [1].

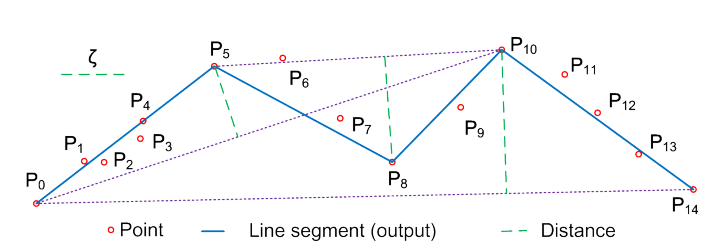
I implement the Douglas-Peucker algorithm using C#.

Here is my code. (Github: https://github.com/IrisLoveLeo/DouglasPeucker )

using System;
using System.Collections.Generic;
using System.Linq;

namespace Statistics
{
    public class DouglasPeucker
    {
        private List<Point> _pointsList;
        private double _errorBound; // degree
        public DouglasPeucker(List<Point> pointsList, double errorBound)
        {
            _pointsList = new List<Point>();
            if (pointsList != null)
            {
                Point last = pointsList.First();
                _pointsList.Add(last);

                for (int i = 1; i < pointsList.Count; i++)
                {
                    if (!last.Equals(pointsList[i]))
                    {
                        _pointsList.Add(pointsList[i]);
                        last = pointsList[i];
                    }
                    else
                    {
                        Console.WriteLine("丢弃相同的点：" + last);
                    }
                }
            }
            _errorBound = errorBound;
        }

        public List<Point> Compress()
        {
            if (_pointsList == null || _pointsList.Count <= 2)
            {
                return _pointsList;
            }

            List<Point> result = CompressHelper(_pointsList);
            result.Add(_pointsList.Last());

            return result;
        }

        private List<Point> CompressHelper(List<Point> pointsList)
        {
            if (pointsList.Count < 2)
            {
                return pointsList;
            }
            
            List<Point> result = new List<Point>();

            // 有可能是polygon
            if (pointsList.First().Equals(pointsList.Last()))
            {
                var r1 = CompressHelper(pointsList.GetRange(0, pointsList.Count / 2));
                var r2 = CompressHelper(pointsList.GetRange(pointsList.Count / 2, pointsList.Count - pointsList.Count / 2));
                result.AddRange(r1);
                result.AddRange(r2);
                return result;
            }

            Line line = new Line() { p1 = pointsList.First(), p2 = pointsList.Last() };

            double maxDistance = 0;
            int maxIndex = 0;

            for (int i = 1; i < pointsList.Count - 1; i++)
            {
                var distance = Distance(pointsList[i], line);
                if (distance > maxDistance)
                {
                    maxDistance = distance;
                    maxIndex = i;
                }
            }

            if (maxDistance <= _errorBound)
            {
                result.Add(pointsList.First());
            }
            else
            {
                var r1 = CompressHelper(pointsList.GetRange(0, maxIndex));
                var r2 = CompressHelper(pointsList.GetRange(maxIndex + 1, pointsList.Count - maxIndex - 1));
                result.AddRange(r1);
                result.Add(pointsList[maxIndex]);
                result.AddRange(r2);
            }

            return result;
        }

        private double Distance(Point p, Line line)
        {
            var p1 = line.p1;
            var p2 = line.p2;
            return Math.Abs(
                    ((p2.Lng - p1.Lng) * p.Lat + (p1.Lat - p2.Lat) * p.Lng + (p1.Lng - p2.Lng) * p1.Lat + (p2.Lat - p1.Lat) * p1.Lng) /
                    Math.Sqrt((p2.Lng - p1.Lng) * (p2.Lng - p1.Lng) + (p1.Lat - p2.Lat) * (p1.Lat - p2.Lat))
                );
        }
    }

    public class Point
    {
        public double Lat { set; get; }
        public double Lng { set; get; }
        public bool Equals(Point p)
        {
            return Lat == p.Lat && Lng == p.Lng;
        }
        override
        public string ToString()
        {
            return "[" + Lat + "," + Lng + "]";
        }
    }

    class Line
    {
        public Point p1 { set; get; }
        public Point p2 { set; get; }
    }
}

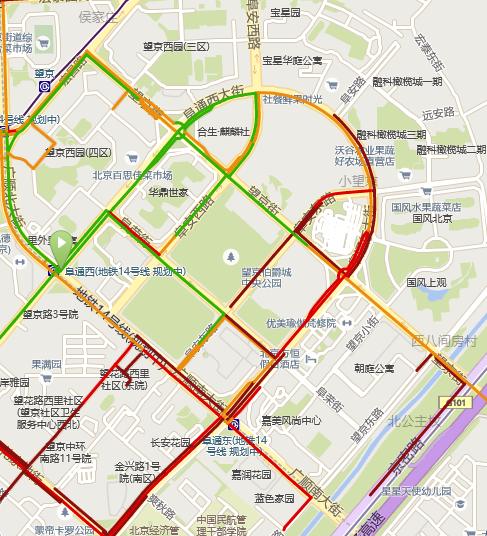
Here is the effect of the DP on road network compress.

Before Compress:

After Compress:

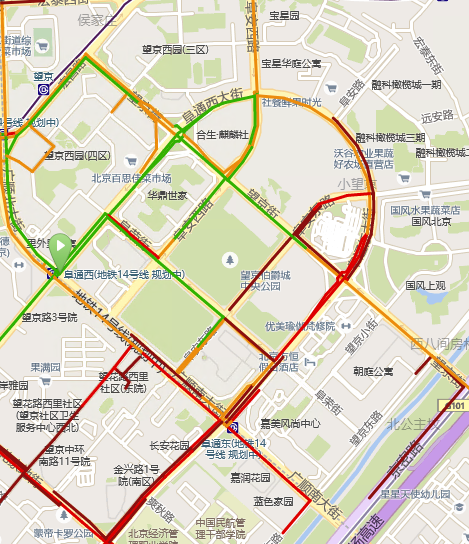
The road network file size has been reduced to half.

[1] Lin X, Ma S, Zhang H, et al. One-pass error bounded trajectory simplification[J]. Proceedings of the VLDB Endowment, 2017, 10(7): 841-852.